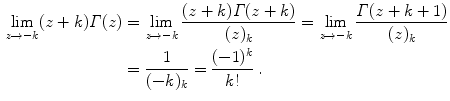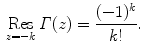Wolfram Koepf - Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities
Here you can read online Wolfram Koepf - Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2014, publisher: Springer, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities
- Author:
- Publisher:Springer
- Genre:
- Year:2014
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Modern algorithmic techniques for summation, most of which were introduced in the 1990s, are developed here and carefully implemented in the computer algebra system Maple.
The algorithms of Fasenmyer, Gosper, Zeilberger, Petkovek and van Hoeij for hypergeometric summation and recurrence equations, efficient multivariate summation as well as q-analogues of the above algorithms are covered. Similar algorithms concerning differential equations are considered. An equivalent theory of hyperexponential integration due to Almkvist and Zeilberger completes the book.
The combination of these results gives orthogonal polynomials and (hypergeometric and q-hypergeometric) special functions a solid algorithmic foundation. Hence, many examples from this very active field are given.
The materials covered are suitable for an introductory course on algorithmic summation and will appeal to students and researchers alike.
Wolfram Koepf: author's other books
Who wrote Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities? Find out the surname, the name of the author of the book and a list of all author's works by series.










![Magnus Lie Hetland [Magnus Lie Hetland] - Python Algorithms: Mastering Basic Algorithms in the Python Language, Second Edition](/uploads/posts/book/124062/thumbs/magnus-lie-hetland-magnus-lie-hetland-python.jpg)

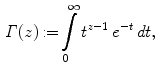
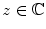 with
with 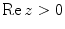 (or, if you prefer only to think of real variables, for real
(or, if you prefer only to think of real variables, for real 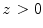 ). Using integration by parts, we get the fundamental functional equation
). Using integration by parts, we get the fundamental functional equation 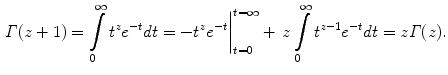
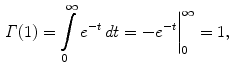
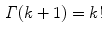
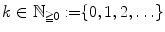 . Therefore the
. Therefore the 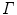 -function interpolates the factorial function continuously, and we may define the factorial function by (
-function interpolates the factorial function continuously, and we may define the factorial function by (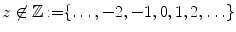 with nonpositive real part one reads the fundamental functional equation () from right to left to obtain
with nonpositive real part one reads the fundamental functional equation () from right to left to obtain 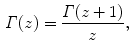
 -function by a recursive application of this rule for
-function by a recursive application of this rule for  with nonpositive real part (in particular for
with nonpositive real part (in particular for 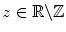 with
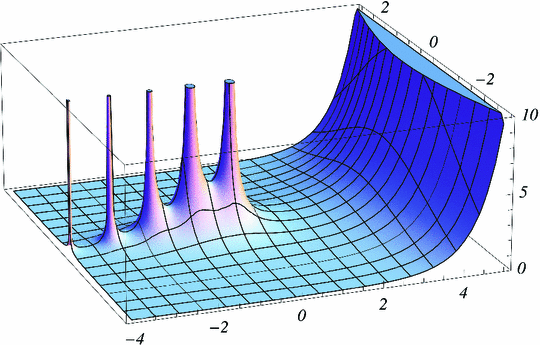
with 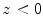 ) (Figs. ).
) (Figs. ). 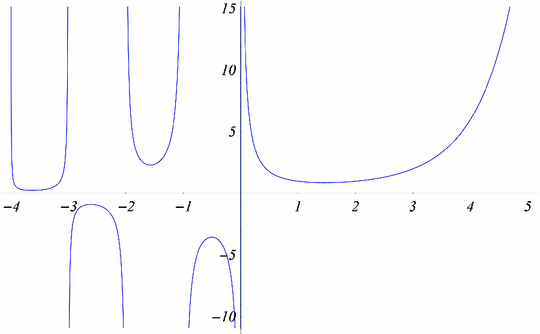
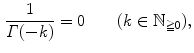
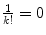 for
for 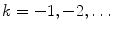 . In function-theoretic terms this means that the function
. In function-theoretic terms this means that the function 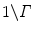 is an entire function, i.e., it is analytic in the entire complex plane with zeros exactly at the negative integers and the origin, the poles of
is an entire function, i.e., it is analytic in the entire complex plane with zeros exactly at the negative integers and the origin, the poles of 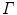 .
.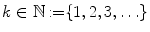
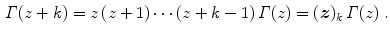
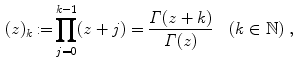
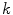 .
.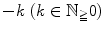 of the
of the 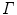 -function
-function