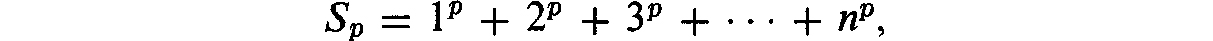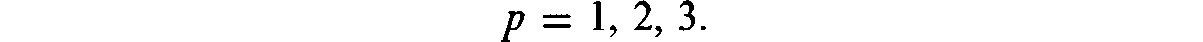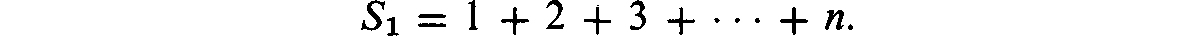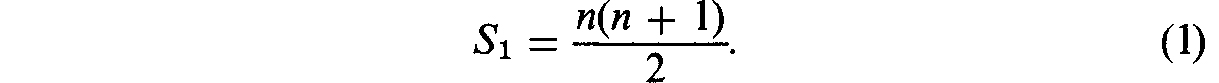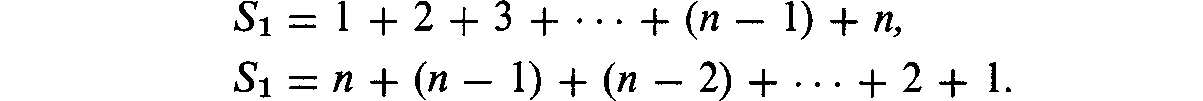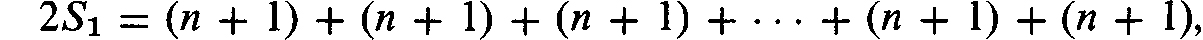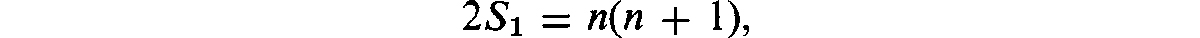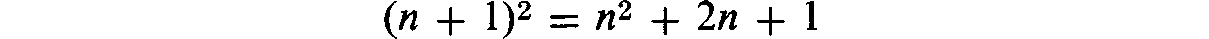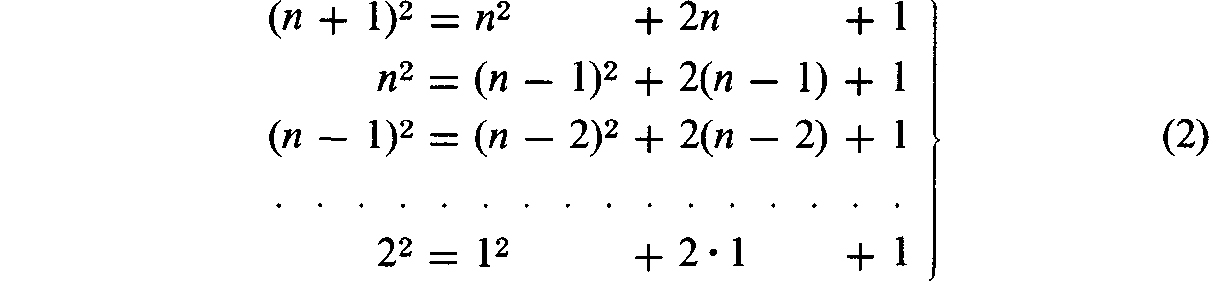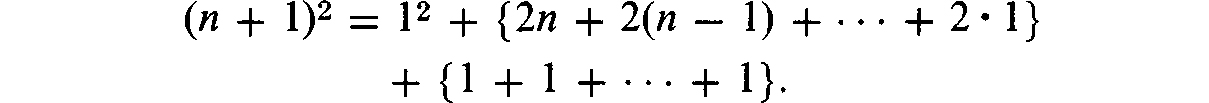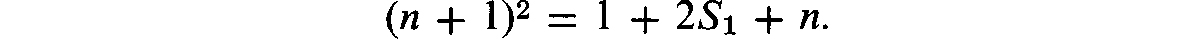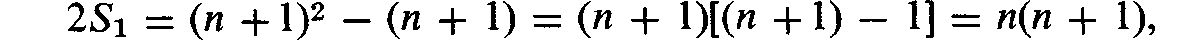I.P. Natanson - Summation of Infinitely Small Quantities

Summation of Infinitely Small Quantities

Bibliographical Note

This Dover edition, first published in 2020, is an unabridged republication of the work originally published in 1963 by D. C. Heath and Company, Boston, as part of the "Topics in Mathematics" series. It was translated and adapted from the 1960 third Russian edition by Stephen Whelan and Coley Mills, Jr.

Library of Congress Cataloging-in-Publication Data

Names: Natanson, I. P. (Isidor Pavlovich), author.

Title: Summation of infinitely small quantities / I.P. Natanson.

Other titles: Summirovanie beskonechno malykh velichin. English

Description: Mineola, New York : Dover Publications, Inc., 2020. | This Dover edition, first published in 2020, is an unabridged republication of the work originally published in 1963 by D. C. Heath and Company, Boston, as part of the "Topics in Mathematics" series. It was translated and adapted from the 1960 third Russian edition by Stephen Whelan and Coley Mills, Jr. | Summary: "Translated and adapted from a popular Russian educational series, this concise book requires only some background in high school algebra and elementary trigonometry. It explores the fundamental concept of the integral calculus: the limit of the sum of an infinitely increasing number of infinitely decreasing quantities. Mastery of this concept enables the solution of geometry and physics problems and introduces the systematic study of higher mathematics" Provided by publisher.

Identifiers: LCCN 2019054432 | ISBN 9780486843377 (trade paperback)

Subjects: LCSH: Calculus, Integral.

Classification: LCC QA308 .N313 2020 | DDC 515/.43dc23

LC record available at https://lccn.loc.gov/2019054432

Manufactured in the United States by LSC Communications

84337801

www.doverpublications.com

2 4 6 8 10 9 7 5 3 1

2020

PREFACE TO THE AMERICAN EDITION

IN ITS PRESENT FORM, integral calculus is a rather complex subject, since it is the result of an interplay of many very different ideas. Nevertheless, the fundamental concept upon which the integral calculus is built is quite simple and natural and was in essence known in antiquity. It is the concept of the "limit of the sum of an infinitely increasing number of infinitely decreasing quantities."

Mastering this concept is very useful, since it allows the solution of a number of important problems in geometry and physics, permits a deeper grasp of the idea of a limit, and serves as an excellent introduction to the systematic study of higher mathematics.

This booklet presents implications of this concept and their use in the solution of various concrete problems. For the first five chapters the reader should have a background of two years of high school algebra. A knowledge of elementary trigonometry is needed for an understanding of the last chapter.

CONTENTS

Summation of Infinitely Small Quantities

1. Some Algebraic Formulas

. INTRODUCTION

In the presentation which follows, we shall need certain formulas, algebraic in nature, which are not always explained at school. These formulas give expressions for sums of the form

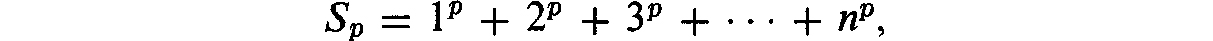
where p and n denote positive whole numbers, and where the dots indicate that we keep adding the numbers 1p, 2p, 3p, etc., until we reach np. We require expressions for the sum Sp only for small values of p:

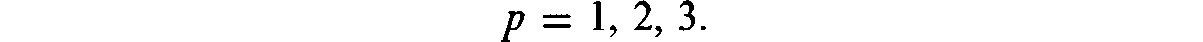
Let us derive these formulas.

. THE SUM OF THE FIRST n NATURAL NUMBERS

Let us find, first of all, the sum

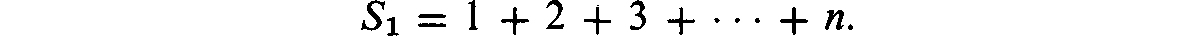
This sum is the sum of n terms of the arithmetic progression whose first term is a1 = 1 and whose difference is d = 1; its value, therefore, can be determined with the help of the well-known algebraic formula

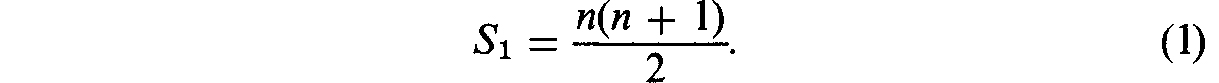
This formula can be derived as follows:

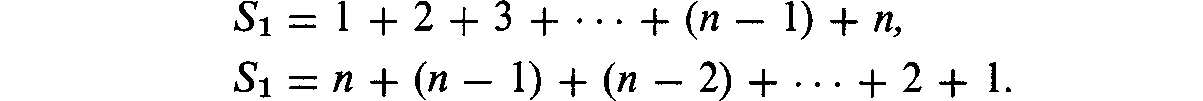
Adding these two equations term by term, we get

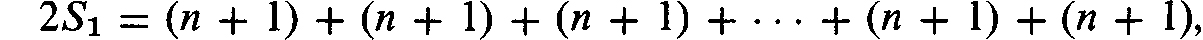
so that

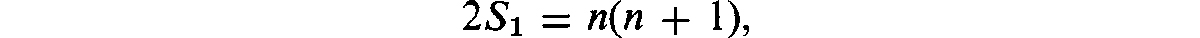
from which formula () follows immediately.

We shall indicate another method for deriving formula (), which, although a little more complicated than the method just employed, can be applied very well for finding any sum Sp in the derivation of formulas Sp (even when p is greater than 1). Let us consider the equality

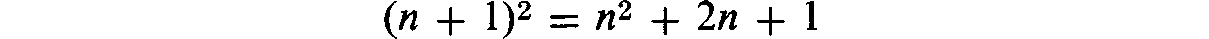
and in it successively replace n by n 1, then by n 2, and so on until we reach 1. As a result we obtain a whole series of equalities

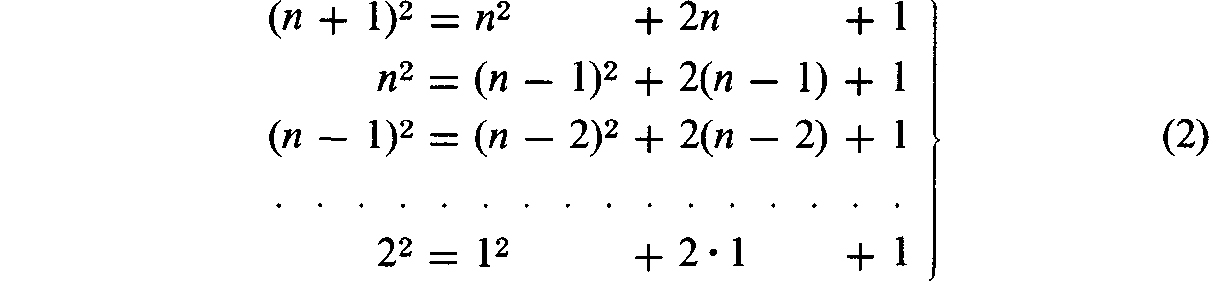
Let us add all these equalities. Notice that the column of terms on the left-hand side will be composed of almost the same terms as the column of first terms on the right-hand side. The only differences between the two columns are these: the term 12, which stands last in the column on the right, does not appear in the left column; and the term (n + 1)2, which stands first in the left column is absent from the right side.

Having made this observation, we see that, cancelling the same terms of both columns, we get

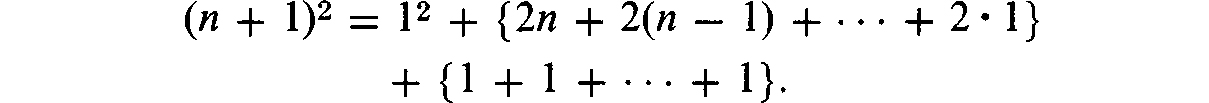
The number of terms in the second pair of braces is equal to the number of equalities in system (by the first pair of braces, the expression remaining in the braces is precisely the sum S1. If we further replace 12 by 1, we get

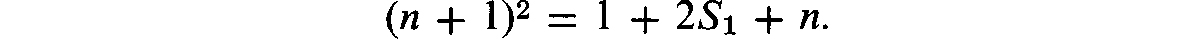
Hence,

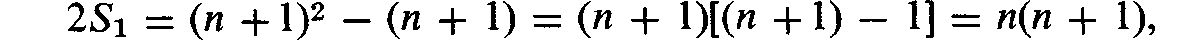
and, finally,

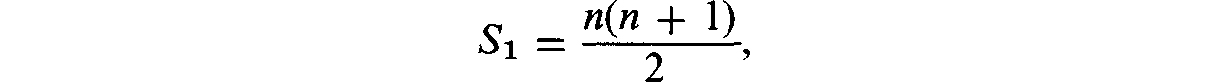
so that we get formula () again.

. THE SUM OF THE SQUARES