Top 10 codinginterview problemsasked in Googlewith solutions
Algorithmic Approach
Lin Quan
2014 Lin Quan. All Rights Reserved.
Preface
This book is written for helping people prepare forGoogle Coding Interview. It contains top 10 programming problemsfrequently asked @Google with detailed worked-out solutions bothin pseudo-code and C++(and C++11).It came out as a result of numerous requests received from codersacross the Globe, primarily from Google aspirants. Author has avast collection of algorithmic problems since 20 years includingexperience in preparing computer science students for participationin programming contests like TopCoder, ACM ICPC and others.For suggestions, feedback and comments, the author can becontacted at : lin.quan.20@gmail.com
Lin Quan
Retired Professor(Computer Science)
March 7, 2014
List of Chapters
1.1
1.2
1.2.1
1.2.2
1.3
1.3.1
1.3.2
1.4
1.5
1.6
2.1
2.2
2.3
2.4
2.5
2.6
2.6.1
2.6.2
2.7
2.7.1
2.7.2
2.7.3
2.8
3.1
3.2
3.2.1
3.2.1.1
3.2.2
3.2.3
3.3
3.3.1
3.3.1.1
3.3.1.2
3.4
4.1
4.1.1
4.1.2
4.2
4.2.1
4.2.2
4.2.3
4.3
4.4
4.5
4.6
5.1
5.2
5.3
5.4
5.5
6.1
6.2
6.3
6.3.1
6.4
7.1
7.2
7.2.1
7.2.2
7.3
7.3.1
7.3.1.1
7.3.2
7.3.3
7.3.4
7.3.5
7.4
8.1
8.1.1
8.1.2
8.1.3
8.1.4
8.1.5
8.1.6
8.1.7
8.1.8
8.2
8.2.1
8.2.2
8.2.3
8.2.4
8.3
9.1
9.1.1
9.1.2
9.2
9.2.1
9.2.2
9.2.3
10.1
10.1.1
10.1.2
10.1.3
10.1.4
10.1.5
10.1.6
10.2
10.3
*
List of Algorithms
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
List of listings
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
*
Chapter 1
Matching Nuts and Bolts Optimally
Problem1 ( G. J. E. Rawlings )
There is a bag full of n nuts and n bolts, each of distinct sizes, such that there is one-to-one correspondence between the nuts and the bolts, i.e., for every nut, there is a bolt and vice verse. Nuts cannot be compared to nuts and bolts cannot be compared to bolts directly, but nuts can be compared to bolts by trying to fit one into the other. Design and implement an optimal algorithm for fitting all nuts to bolts. By optimal we mean to minimize the number of comparisons involved in the algorithm.
Solution
1.1 Basic Analysis
The same problem can be posed to a computer scientist asfollows:
Given two sets B : { b , ,b n } and N : { n , ,n n } , where B is a set of n distinct real numbers (representing the sizes of the bolts) and N is a permutation of B , we wish to find efficiently the unique permutation N n so that b i = n ( i ) i , based on queries of the form compare b i and n j . The answer to each such query is either
- b i > n j or
- b i = n j or
- b i < n j
Since there are n! possibilities for , the obvious information theoreticlower bound shows that any bounded degree decision tree thatsolves the problem has depth at least log ( n !).
Using Sterlings approximation :
log ( n !) ( n log n )
Similar to comparison-based sorting, it can be analyzed usingdecision tree. Please note that we can model any algorithm formatching nuts and bolts as a decision tree.
The tree will be a ternary tree , since every comparison has three possible outcomes:
- less than ,
- equal , or
- greater than
The height of such a tree corresponds to the worst-case number ofcomparisons made by the algorithm it represents, which in turn is alower bound on the running time of that algorithm. We thereforewant a lower bound of ( n log n ) on the height, H , of any decisiontree that solves nuts n bolts problem mentioned in earliersection.
To begin with, note that the number of leaves L in any ternarytree must satisfy L 3 H . Next, consider the following class ofinputs.
Let the input array of nuts N be fixed and consist of n nuts inincreasing sorted order, and consider one potential input for everypermutation of the bolts. In order to match the nuts and bolts,our algorithm must in this case essentially sort the array ofbolts.
In our decision tree, if two different inputs of this typewere mapped to the same leaf node, our algorithm wouldattempt to apply to both of these the same permutation ofbolts with respect to nuts, and it follows that the algorithmcould not compute a matching correctly for both of theseinputs.
Therefore, we must map every one of these n! different inputs toa distinct leaf node, i.e.
L n !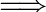 3 H n !
3 H n !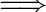 H log n
H log n 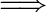 H = ( n log n )
H = ( n log n )
Please note that base of logarithm doesnt matter in complexity,it is a kind of constant, so we will ignore this too.
In particular, at least ( n log n ) comparisons are needed. This isa lower bound for the expected number of comparisons in anyrandomized algorithm for the problem as well.
A simple modification of Randomized Quicksort shows thatthere are simple randomized algorithms whose expected number ofcomparisons (and running time) are O ( n log n ):
- pick a random bolt
- compare it to all the nuts
- find its matching nut, thus splitting the nuts into three parts:
- nuts smaller for the bolt
- nuts exactly fit with the bolt
- nuts bigger for the bolt
- compare the matching nut found above to rest of the remaining n - 1 bolts, thus splitting the bolts into three parts:
- bolts looser for the nut
- bolt exactly fit to the nut
- bolts tighter for the nut
- thus splitting the problem into two problems, one consisting of the nuts and bolts smaller than the matched pair and one consisting of the larger ones.
This pair of partitioning operations can easily implemented in( n ) time, and it leaves the nuts and bolts nicely partitioned sothat the pivot nut and bolt are aligned with each-other and allother nuts and bolts are on the correct side of these pivots:
- smaller nuts and bolts precede the pivots, and
- larger nuts and bolts follow the pivots.
This algorithm then finishes by recursively applying itself to thesubarrays to the left and right of the pivot position to match theseremaining nuts and bolts. We can assume by induction on n that these recursive calls will properly match the remainingbolts.
To analyze the running time of this algorithm, we can use thesame analysis as that of randomized quicksort . We are performinga partition operation in ( n ) time that splits our probleminto two subproblems whose sizes are randomly distributedexactly as would be the subproblems resulting from a partitionin randomized quicksort. Therefore, applying the analysisfrom quicksort, the expected running time of our algorithm is( n log n ).
This problem provides a striking example of how randomizationcan help simplify the task of algorithm design.
Rawlins [] posed this problem as :
We wish to sort a bag of n nuts and n bolts by size in the dark. We can compare the sizes of a nut and a bolt by attempting to screw one into the other. This operation tells us that either the nut is bigger than the bolt; the bolt is bigger than the nut; or they are the same size (and so fit together). Because it is dark we are not allowed to compare nuts directly or bolts directly. How many fitting operations do we need to sort the nuts and bolts in the worst case?






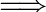 3 H n !
3 H n ! H log n
H log n  H = ( n log n )
H = ( n log n )