John Gribbin - Science: A History in 100 Experiments

JOHN GRIBBIN gained a PhD from the Institute of Astronomy in Cambridge (then under the leadership of Fred Hoyle), before working as a science journalist for Nature and later New Scientist.

MARY GRIBBIN is a teacher with a special gift for communicating difficult concepts, and she is a previous winner of the TES Junior Information Book Award. They have co-written several titles for adults and children. John has written many bestselling popular science books, including Erwin Schrdinger and the Quantum Revolution, In Search of the Multiverse and The Universe: A Biography. John and Mary are both Visiting Fellows at the University of Sussex.

The authors thank the Alfred C. Munger Foundation for financial support, and the University of Sussex for providing a base from which to work.

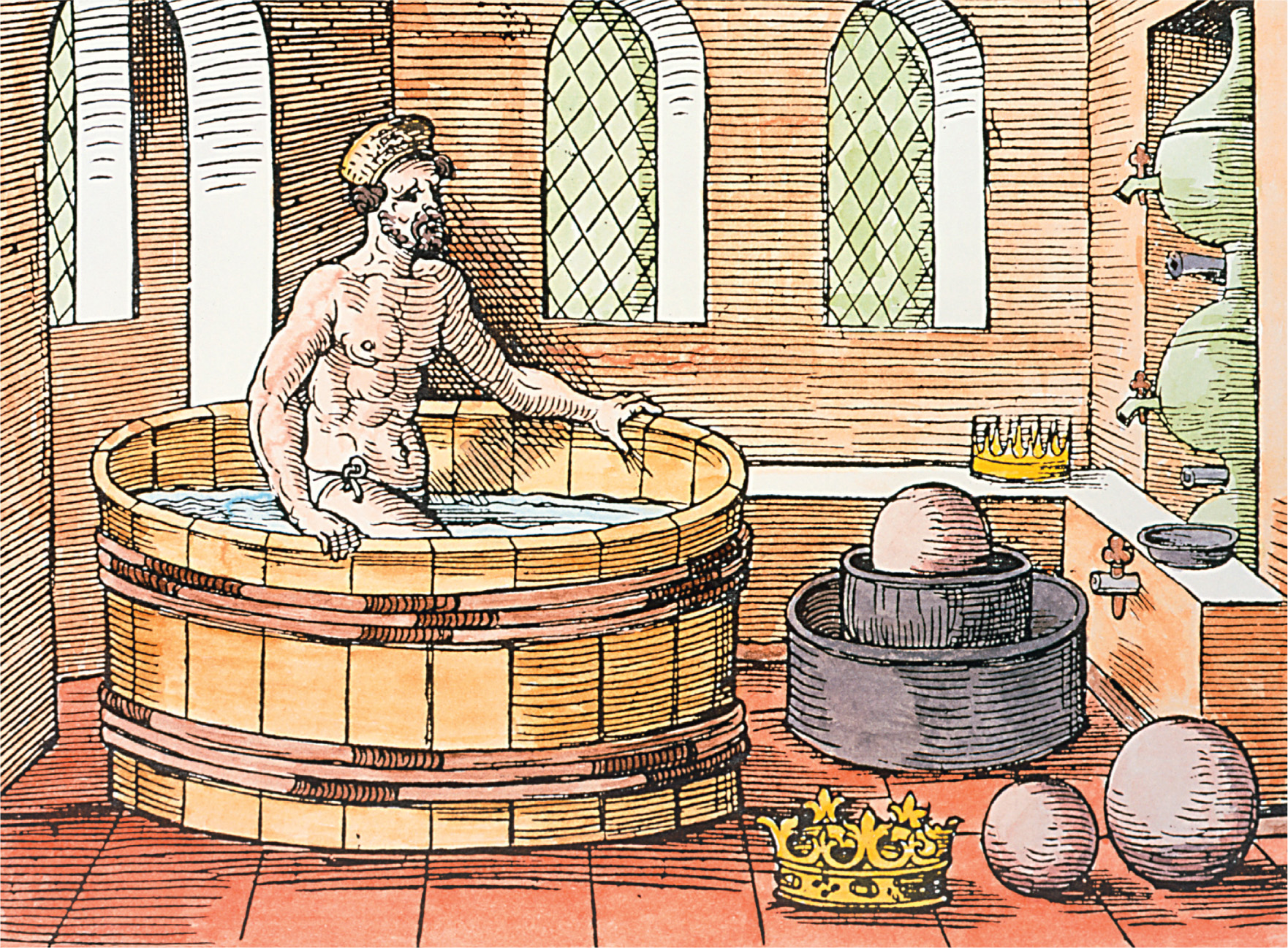
One of the first, and most famous, scientific experiments was carried out by Archimedes, who lived in the third century BC . Not much is known about Archimedes personal life, but it seems that he was a relative of King Hieron II of Syracuse, in Sicily, and, after extensive travels, he settled down as the Kings astronomer and mathematician. According to legend, King Hieron had a new crown, probably in the form of a laurel wreath, made for him from a bar of gold he supplied to the jeweller, to give as an offering to the gods in a temple. He suspected that the jeweller had kept some of the gold and mixed in cheaper silver instead to make up the same weight for the crown. This would be a doubly serious matter; not only would the king be cheated, but the gods might be offended at being given an inferior offering. So Hieron ordered Archimedes to find out if the crown was made of pure gold without, of course, damaging it in any way. Archimedes had no idea how to do this, and worried about the problem for days. Then, when stepping in to a bath filled to the brim, he noticed how the water slopped over the side as it was displaced by his body. The story has come down to us from Vitruvius, a Roman architect, in a book written two centuries after Archimedes had died. We do not know where he got it from, but this is where we get the image of Archimedes immediately realizing how to test the crown, and becoming so excited that he ran out into the street, naked and wet, shouting Eureka! (I have found it!).

Science Photo Library
An imaginative portrayal of the Greek mathematician and physicist Archimedes (287212 BC ) in his bath. Archimedes showed that an object immersed in a fluid is supported with a force equal to the displaced fluids weight (Archimedes principle).

What Archimedes had realized was that the volume of water displaced from the bath was equal to the volume of his body immersed in the water. As silver is less dense than gold, if the crown were made of a mixture of silver and gold it would have to be bigger than a crown made of pure gold in order to have the same weight. And he could measure the volume of the crown, without damaging it, by immersing it in water and seeing how much water was displaced.

Nobody knows exactly how Archimedes carried out the experiment. But the most likely method is based on an observation he described in his book, On FloatingBodies. There, Archimedes explained that the upward force (buoyancy) exerted on an object placed in water (or any other fluid) is equal to the weight of fluid that is displaced. This is now known as Archimedes Principle. And, of course, the weight of water displaced will be proportional to the volume of water displaced.

The obvious way to use this to test the purity of the crown, as Archimedes must have realized, would be to balance the crown against exactly the same weight of pure gold on a beam balance above a tank of water. Then, the balance is lowered until the crown and the pure gold sample are immersed in the water, while the balance arm stays above it. If both objects are made of pure gold, they will each displace the same volume (and therefore the same weight) of water, experience the same buoyancy force, and stay in balance. But if the crown is less dense than gold it will have a bigger volume, displace more water, and be more buoyant than the pure gold, so the balance will tip down on the side of the gold. The beauty of this experiment is that you dont actually have to measure the volume of the crown, or the volume of water that it displaces; you just watch to see if the balance tilts.

That, it seems, is exactly what happened. Archimedes did the experiment (or something very similar) and found that the jeweller had indeed cheated the king. About five centuries after Vitruvius, the story was re-told in a Latin poem Carmen de ponderibus et mensuris which described the use of such a hydrostatic balance, and in the twelfth century a manuscript called Mappae clavicula gave detailed instructions on how to make weighings in this way to calculate the proportion of silver in the adulterated crown.

Archimedes Principle also explains why a ship made of steel can float. A solid lump of steel displaces a relatively small amount of water, much less than its own weight, and sinks. But if the same amount of steel is spread out in the shape of a boat, or even a simple bowl (like a coracle), a larger volume of water is displaced, weighing more than the weight of the steel, resulting in a large enough upwards force to make the boat float.

The first scientific attempt to measure the size of the Earth was made by a Greek polymath, Eratosthenes of Cyrene (276194 BC ), who was in charge of the Library of Alexandria in the third century BC . He was a contemporary and friend of Archimedes. His experiment involved some observations of his own, made in Alexandria, but combined with evidence from a far away place, the city then known as Syene (now Aswan), which he had never visited.

Eratosthenes learned that each year on the day of the summer solstice, when the Sun is at its highest in the sky, it was exactly overhead at Syene, south of Alexandria. Travellers told how the reflection of the Sun could be seen at the bottom of a deep well in Syene on that day. Even at the summer solstice, the Sun is not directly overhead at Alexandria, because, as Eratosthenes appreciated, the Earth is round. So he made careful measurements of the difference between the angle made by the Sun and the vertical at the time of the solstice, working out that this corresponded to one-fiftieth of a circle, or 7 12 of arc. Simple geometry told him that this meant that the distance from Alexandria to Syene was one-fiftieth of the circumference of the Earth, assuming (which is not quite true) that Syene lies due south of Alexandria.

The distance from Syene to Alexandria was well known even in Eratosthenes day (it is about 800 kilometres in modern units). Egyptian records gave the distance as 5,000 stades, and Eratosthenes checked this by asking camel train drivers how long it took them to make the journey (some sources say he hired a man to pace out the distance; but this may be apocryphal). This gave him a figure of 694 stades per degree, which he rounded off to 700. Multiplying by 360 gave him the circumference of the Earth 252,000 stades (he could have just multiplied 5,000 by 50 to get the answer 250,000, but apparently he did it the hard way).

So what is this in modern units? Unfortunately for us, the Greeks and Egyptians used slightly different stades, but the likelihood is that Eratosthenes, being Greek, used the Greek measurement, where one stade corresponds to 185 metres, which gives a circumference of 46,620 kilometres, only 16.3 per cent too big. In the unlikely event that he used the Egyptian measurement, with one stade corresponding to 157.5 metres, he would have come up with a figure of 39,690 kilometres, just a bit too small (less than 2 per cent smaller than the actual distance, 40,008 kilometres). Either way, it is impressive.