More Great Titles from Batsford
tap to read more



 www.anovabooks.com
www.anovabooks.com

First published by The Crowood Press Ltd in 1984
Reissued by Batsford in 2004
10 Soutcombe Street
London
W14 0RA
An imprint of Anova Books Company Ltd.
Copyright Paul Littlewood 1984, 2004
The right of Paul Littlewood to be identified as Author of this work has been asserted by him in accordance with the Copyright, Designs and Patents Act 1988.
All rights reserved. No part of this publication may be reproduced in any form or by any means without permission from the publisher.
First eBook publication 2013
ISBN 9781849941297
Also availble in paperback
ISBN 9780713489347
This book can be ordered directly from the publisher at
www.anovabooks.com , or try your local bookshop
To JJ and Katy
INTRODUCTION
There are numerous views on the nature of chess. Many people, such as Mikhail Talworld champion 1960-1see it as an art. Other more precise people, such as Mikhail Botvinnikworld champion 1948-57, 1958-60 and 1961-63view it as a science. However, I subscribe to the view of people such as Danish grandmaster Bent Larsen, who believe it to be a battle.
In all battles the commanders must have a strategic plan of action. However, no matter how good the plan, the battle will be lost if the soldiers involved are not capable of carrying it out properly.
Chess is very similar. A player may adopt an excellent strategic plan but can often lose the game because his tactics are deficient.
As an illustration consider the following short game, with my view of Whites possible thoughts as he played each move.
I like this move as it controls the important central square e5 and frees my queen and queens bishop. It is also the favourite first move of my hero Spassky.
| 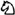 f6 f6 |
| 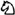 d2 d2 |
I would like to have played 2 e4 controlling more squares but Black would have just captured the pawn. Therefore I will prepare it by guarding the square.
What a stupid move Black has played! I can simply win a pawn for nothing now as well as make him lose time by having to move his knight again.
| 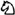 g4 g4 |
Oh, ohI dont like this threatening knight very much. Id better get rid of it before it can do any damage. Unfortunately it will capture the e-pawn but that is probably lost in the long run anyway.
| h3 |
| 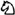 e3 e3 |

Whats this? I can simply take this piece with my f-pawn. I will then be a piece up for nothing. Who is this silly twit with the black pieces anyway? I am surprised the committee let him join the club. Hang on a minute thoughIf I take the knight he plays 5 h4+ 6 g3 (forced) 6
h4+ 6 g3 (forced) 6 xg3 mate. Oh no, what have I done? My queen is attacked and it cannot move. Perhaps if I resign the game quickly and start another, the other club members wont notice.
xg3 mate. Oh no, what have I done? My queen is attacked and it cannot move. Perhaps if I resign the game quickly and start another, the other club members wont notice.
What went wrong for White? In fact, he made an instructive error: pursuing a reasonable strategic plan but failing to cope with the tactics employed by his opponent.
The purpose of this book is to arm you with as much of the tactical chess weaponry that is available so that you will not suffer the same fate as White above.
Each chapter deals with one particular tactical point giving many illustrative examples. To ensure that the reader fully understands each point, there are problems to be solved at the end of each chapter. The solutions to these are at the back of the book.
1 PINS
DEFINITION AND EXAMPLES
In battles an enemy can be pinned down so his movement is restricted. A similar fate can befall a chess piece. Consider the following position which arises after the opening moves:

The black knight on c6 cannot move because his king would then be in check from the white bishop on b5, i.e. the black knight is pinned by the white bishop.
This type of pin is an absolute one because the pinned piece is disallowed from moving by the rules of chess. However, consider the next diagram:

Here the black knight on f6 can move but if it does the white bishop on g5 may capture the black queen, leaving White with a substantial material advantage. Therefore unless Black has a very good reason he will not move his knight on f6 because it is pinned against his queen.
There are many other examples of pins, e.g. Diagrams 4, 5, 6 and 7.



















 www.anovabooks.com
www.anovabooks.com
 f6
f6
 h4+ 6 g3 (forced) 6
h4+ 6 g3 (forced) 6 b5
b5

