Varvoglis - History and Evolution of Concepts in Physics

Springer International Publishing Switzerland 2014

Harry Varvoglis 1

(1)

Abstract

The history of any discipline is always based on written texts. In this way, to restrict ourselves to texts of Antiquity, the history of the Jewish people is based on the books of the Old Testament, the history of the Persian Wars on the books by Herodotus and the history of the Peloponnesian War on the books by Thucydides. Even the history of the Trojan War is based on Homers written work, although this was based, in turn, on earlier oral traditions of the Greeks of Homers time. This rule, of course, cannot find an exemption in the history of physics. This is the main reason why the history of physics, and hence the evolution of concepts in this science, necessarily starts from the ancient Greeks. It is certain that other people of historical times were also involved in scientific activities, such as the Babylonians, who developed astronomy, and the Egyptians, who developed geometry. But their aim was to solve practical problems of their everyday life and not to understand nature and its laws. The geometry of the ancient Egyptians was developed for the purpose of redistributing land after the annual flooding of Nile, while Babylonian astronomy was limited to the simple recording of astronomical observations, with a few surviving examples of predictions of future events. Instead, the interpretation of nature and its laws, in both these nations, was the responsibility of priests and kings. In other words, the interpretation of nature for them was not a result of rational thinking; it was based on truth by revelation. The truth was revealed to rulers, nobles and priests, and accepted, without questioning, by the rest of the people. This truth was closely related to the religion of each nation.

The history of any discipline is always based on written texts. In this way, to restrict ourselves to texts of Antiquity, the history of the Jewish people is based on the books of the Old Testament, the history of the Persian Wars on the books by Herodotus and the history of the Peloponnesian War on the books by Thucydides. Even the history of the Trojan War is based on Homers written work, although this was based, in turn, on earlier oral traditions of the Greeks of Homers time. This rule, of course, cannot find an exemption in the history of physics. This is the main reason why the history of physics, and hence the evolution of concepts in this science, necessarily starts from the ancient Greeks. It is certain that other people of historical times were also involved in scientific activities, such as the Babylonians, who developed astronomy, and the Egyptians, who developed geometry. But their aim was to solve practical problems of their everyday life and not to understand nature and its laws. The geometry of the ancient Egyptians was developed for the purpose of redistributing land after the annual flooding of Nile, while Babylonian astronomy was limited to the simple recording of astronomical observations, with a few surviving examples of predictions of future events. Instead, the interpretation of nature and its laws, in both these nations, was the responsibility of priests and kings. In other words, the interpretation of nature for them was not a result of rational thinking; it was based on truth by revelation. The truth was revealed to rulers, nobles and priests, and accepted, without questioning, by the rest of the people. This truth was closely related to the religion of each nation.

One can find indications of this mode of thinking in Greek mythology, where it is stated that lightning is cast by Jupiter, earthquakes are caused by Hephaestus and storms are raised by Poseidon with his trident. Generalizing this way of thinking, one may conclude that any phenomenon, even the simplest one, such as the motion of bodies, is caused by a god. But in the late 7th century BC there were Greeks who believed that interpretations of this sort were not very reasonable. So, they tried to explain natural phenomena through a system of rational reasoning. This system was called natural philosophy and those who were practicing it were called natural philosophers. ). From the above philosophers, Thales and Pythagoras did not leave behind any written text, while the others wrote books, which unfortunately were lost, except for several extensive excerpts of the books of the latter two (Empedocles and Parmenides). Thus, almost all available information about the ideas of natural philosophers of the 6th century BC is based on brief references to their work, found in books of later authors.

The method followed by the first natural philosophers to explain natural phenomena proved to be extremely successful and was used by all scientists-researchers until the Renaissance. This method seemed more or less similar to the logical method, which was introduced many years later (in the Hellenistic era) and in a more sophisticated form by Euclid of Alexandria (ca. 325 BCca. 265 BC) in developing geometry. The Greek natural philosophers started from a postulate , which seemed more or less self-evident, and continued with the logical conclusions that could be drawn from it. All conclusions that could be drawn from a set of initial postulates formed a theory . The initial postulate, which seems obvious but cannot be proven, in philosophy is called a hypothesis (in mathematics, it is called assumption or axiom ). In literature, one can often come across other terms with the same meaning, like conjecture and (in German) Ansatz .

The truth of an axiom cannot be proven within the framework of the theory which is based and developed on it. However, the axiom may be verified by showing that the theory, which is developed on it, is consistent with relevant experiments or observations. For example, one of the fundamental axioms of Euclids geometry is that two parallel lines do not intersect . This axiom seems obvious, but as understood by later mathematicians, this holds true only in flat spaces. 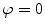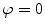The surface of the Earth is not flat but curved and that is why two adjacent meridians, which are parallel on the equator (i.e., for a latitude ), intersect at the poles. Therefore, Euclidean geometry holds only approximately on the surface of the Earth and only for relatively small distances. When the dimensions of geometric drawings we study on its surface are of the order of hundreds of kilometers or more, then deviations from the Euclidean geometry start to appear, such as the fact that the sum of the angles of a triangle is greater than 180. Therefore, we arrive to the conclusion that an axiom can provide a correct theory under certain conditions and a wrong one under others. Today, the criterion for accepting a theory, and consequently the axioms on which it is based, is the experimental verification of the predictions arising from it. Using this method, we can prove that a theory is wrong, but we can never prove that it is correct! In simple terms, if experiments are consistent with the theory, then we continue to use it. But if they do not agree, then we reject the theory and the axioms on which it is based, and introduce new axioms. As discussed in the book, this has happened several times in the recent history of physics, but not in ancient times.