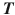It has become apparent in recent decades that in discussing fundamental properties of space and time the adequate language is Lorentzian geometry. Correspondingly, we start the book with a brief introduction to that discipline. In the first four sections of this chapter some basic notionssuch as convexity, causal simplicity, and global hyperbolicityare defined and some basic facts about them are provided, such as Whiteheads and Gerochs theorems, the Gauss lemma, etc. Of course, this recapitulation cannot substitute a systematic presentation, so wherever possible the proofs of those facts are dropped, which is understood as the reference to classical monographs such as [141] or [76]. Then, in Sect. in Chap. 5, but, as it seems, it is interesting also by itself (the perfectly simple sets are as nice as possiblethey are both convex and globally hyperbolic, which makes them exceptionally useful in proving statements).
Finally, in Sect. the cut-and-paste surgery is rigorously described. This is necessary because we shall widely employ that surgery in constructing spacetimes from more simple ones. And experience suggests that even though the method seems simple and pictorial, neglecting some its subtleties may lead to serious mistakes.
Thus, this chapter is technical and a reader can safely skip it or use it as a glossary, if they do not intend to analyse the proofs of the statements formulated in the consequent chapters.
Spacetimes
Classical general relativity, as it is understood in this book, is the theory describing the universe by an (inextendible, see below) spacetime
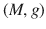
, which is a connected Hausdorff manifold M endowed with a smooth Lorentz metric
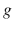
and a time orientation. Sometimes, when it is obvious or irrelevant what metric
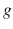
is meant, the manifold M itself will be also called a spacetime.
Comments 1
(1) A rigorous definition of time orientation can be found in [141]. Roughly speaking, it is a choicemade in a smooth mannerof which timelike vectors, see Definition , are future- and which are past-directed. (2) M is automatically smooth and paracompact. For the proof of the latter, non-trivial, fact see [61].
For building a full-fledged theory, the geometrical description must be supplemented with postulates determining how matter acts on geometry (usually these are Einsteins equations) and, conversely, how matter is acted upon by non-trivial geometry (typically the comma-goes-to-semicolon rule is adopted, see Sect. 16 of [135]). Those postulates are of secondary importance. For slightly varying them (introducing, say, a small

-term), one typically changes the theory inconsiderably (at least at non-cosmological scale). At the same time, none of the above-listed properties defining the spacetime can be dropped without mutilating the theory beyond recognition.
A spacetime does not have to describe the whole universe . It is easy to check that any open connected subset of a spacetime is a spacetime too. However, as the Minkowski space exemplifies, the converse is false: even a noncompact spacetime may not be a part of a larger one.
Definition 2
A spacetime
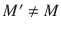
is called an extension of a spacetime M , if the latter is an open subset of the former or is isometric to such a subset. M is extendible , if it has an extension and inextendible , or maximal , otherwise.
Remark 3
An open subset
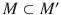
is more than just a spacetime. It is a spacetime imbedded in
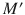
b y a particular isometry. In considering such an imbedded spacetime, we may be interested both in properties defined by its geometry (we shall call such properties intrinsic , see below) and those defined by the imbedding. With this in mind, we shall not automatically identify spacetimes only because they are isometric.
It seems natural to interpret an extension of M as describing a larger than M portion of the universe and to consider M an adequate model of the universe only if it is inextendible. In doing so, however, one encounters some technical problems associated with infinities. For example, the regions
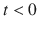
and
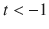
of the Minkowski space are each others extensions. To avoid such problems, it is convenient to consider not spacetimes, but triples
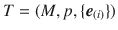
, where p is a point of M , and
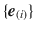
is a basis in the space tangent to M in p . A triple
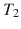
will be called an extension of
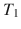
, if there is an isometry
sending
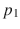
to
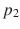
so that the differential
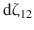
maps
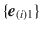
to
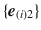
. Such an isometry, if it exists, is unique, which makes theobviously transitiverelation to be an extension of asymmetric on the set of the triples. Thus, the relation in question is a (strict) partial order [87], which enables one to show [62] that any spacetime has a maximal extension (we shall use the same line of reasoning in Chap..











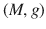 , which is a connected Hausdorff manifold M endowed with a smooth Lorentz metric
, which is a connected Hausdorff manifold M endowed with a smooth Lorentz metric 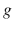 and a time orientation. Sometimes, when it is obvious or irrelevant what metric
and a time orientation. Sometimes, when it is obvious or irrelevant what metric 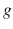 is meant, the manifold M itself will be also called a spacetime.
is meant, the manifold M itself will be also called a spacetime. -term), one typically changes the theory inconsiderably (at least at non-cosmological scale). At the same time, none of the above-listed properties defining the spacetime can be dropped without mutilating the theory beyond recognition.
-term), one typically changes the theory inconsiderably (at least at non-cosmological scale). At the same time, none of the above-listed properties defining the spacetime can be dropped without mutilating the theory beyond recognition.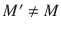 is called an extension of a spacetime M , if the latter is an open subset of the former or is isometric to such a subset. M is extendible , if it has an extension and inextendible , or maximal , otherwise.
is called an extension of a spacetime M , if the latter is an open subset of the former or is isometric to such a subset. M is extendible , if it has an extension and inextendible , or maximal , otherwise.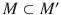 is more than just a spacetime. It is a spacetime imbedded in
is more than just a spacetime. It is a spacetime imbedded in 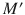 b y a particular isometry. In considering such an imbedded spacetime, we may be interested both in properties defined by its geometry (we shall call such properties intrinsic , see below) and those defined by the imbedding. With this in mind, we shall not automatically identify spacetimes only because they are isometric.
b y a particular isometry. In considering such an imbedded spacetime, we may be interested both in properties defined by its geometry (we shall call such properties intrinsic , see below) and those defined by the imbedding. With this in mind, we shall not automatically identify spacetimes only because they are isometric.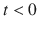 and
and 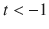 of the Minkowski space are each others extensions. To avoid such problems, it is convenient to consider not spacetimes, but triples
of the Minkowski space are each others extensions. To avoid such problems, it is convenient to consider not spacetimes, but triples 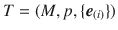 , where p is a point of M , and
, where p is a point of M , and 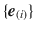 is a basis in the space tangent to M in p . A triple
is a basis in the space tangent to M in p . A triple 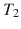 will be called an extension of
will be called an extension of 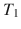 , if there is an isometry
, if there is an isometry 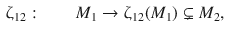
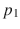 to
to 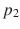 so that the differential
so that the differential 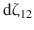 maps
maps 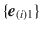 to
to 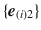 . Such an isometry, if it exists, is unique, which makes theobviously transitiverelation to be an extension of asymmetric on the set of the triples. Thus, the relation in question is a (strict) partial order [87], which enables one to show [62] that any spacetime has a maximal extension (we shall use the same line of reasoning in Chap..
. Such an isometry, if it exists, is unique, which makes theobviously transitiverelation to be an extension of asymmetric on the set of the triples. Thus, the relation in question is a (strict) partial order [87], which enables one to show [62] that any spacetime has a maximal extension (we shall use the same line of reasoning in Chap..