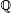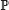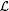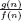Model Risk in
Financial Markets
From Financial Engineering to Risk Management

Model Risk in
Financial Markets
From Financial Engineering to Risk Management
Radu Tunaru
University of Kent, UK

NEW JERSEY LONDON SINGAPORE BEIJING SHANGHAI HONG KONG TAIPEI CHENNAI
Published by
World Scientific Publishing Co. Pte. Ltd.
5 Toh Tuck Link, Singapore 596224
USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601
UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE
Library of Congress Cataloging-in-Publication Data
Tunaru, Radu.
Model risk in financial markets : from financial engineering to risk management / Radu Tunaru
(University of Kent, UK).
pages cm
Includes bibliographical references and index.
ISBN 978-9814663403 (alk. paper)
1. Financial risk management. 2. Risk management. 3. Financial engineering. I. Title.
HD61.T86 2015
332'.0415011--dc23
2015017268
British Library Cataloguing-in-Publication Data
A catalogue record for this book is available from the British Library.
Copyright 2015 by World Scientific Publishing Co. Pte. Ltd.
All rights reserved. This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the publisher.
For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher.
In-house Editor: Li Hongyan
Printed in Singapore
I will never die for my beliefs; because I might be wrong
Bertrand Russell
To my dear daughters Filipa and Joana, who need me to be
always right or at least almost all the time.
Preface
Finance was part of the evolution of humanity for thousands of years. Follow the money and you will understand the course of history. The nascency of mathematics was triggered by the need to solve problems related to money and finance. Modern finance has experienced a meteoric rise in the 1980s, coupled with the introduction of computers on a large scale and also with the liberalization of financial markets. Scientists from many other disciplines like Mathematics, Statistics, Physics, Mechanics, Enginering and Economics, found a new uncharted territory in Modern Finance and they embraced the new gold scientific race.
After a sunrise there is a sunset, and exuberance quite often masks lack of full understanding of the complexity of problems that may surface at any moment in time. The series of crises in Finance culminated with the subprime-liquidity crisis of 2007 that was reminiscent of the financial crash of 1929. Who was to blame and what really happened is still the subject of intensive research, and valuable lessons are to be learned overall.
While everybody is offering an opinion about toxic assets and liquidity measures and trying to design measures of systemic risk impact, not enough attention is paid in my opinion to another source of future problems, that could also reach catastrophic and endemic levels, that is the risk carried by different models, or shortly model risk. What is model risk? Is it important? Can we measure it? These questions will receive a suite of answers in this book but it would be unrealistic to say it covers the entire spectrum of problems related to model risk in financial markets.
This book is written to help graduate students in Finance, MBA and postgraduate students in Quantitative Finance, risk managers, analysts in product control and model validation teams in investment banks, regulators, academics and other parties working as consultants or in rating agencies, understand the difficulty of financial modelling. Since those working with models must have a minimum level of knowledge in quantitative finance I assume that the reader has standard knowledge of probability theory, statistics, econometrics, asset pricing, derivatives, risk management and financial engineering. Financial modelling intrinsically introduces model risk and this book aims to highlight the diversity of model risk facets in finance. It should help the reader develop an inquiring approach when dealing with models in finance.
Radu Tunaru, London 2014
List of Notations
p(t, T) | the price at time t of a zero coupon bond with maturity T |
rt | short rate at time t, unless otherwise stated |
rf | is the continuous-compounding constant risk-free rate per annum |
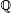
| denotes a generic risk-neutral probability measure, also called martingale pricing measure |
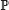
| denotes the physical (also called objective or real-world) probability measure |
{St}t0 | is the stochastic process associated with an asset value |
{Xt}t0 | is the stochastic process associated with an asset value or its return |
L(t; T1, T2) | is the forward Libor rate at time t for the future period [T1, T2] |
VaR(X) | is used for value-at-risk at critical level for the risk of an asset X. Typically = 1%, 5% |
ES(X) | is used for the expected shortfall at critical level for the risk of an asset X |
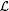
| is the likelihood function |
()+ | = max(, 0)) is the positive part function |
F or FX | is the cumulative distribution function of a random variable X |
is the probability density function of the standard Gaussian distribution |
(a, ) | is the probability density function of the Gaussian distribution with mean a and variance |
is the cumulative probability density function of the standard Gaussian distribution |
a | means distributed asymptotically the same as |
o() | denotes the Little-O Landau notation, so g(n) = o(f(n)) iff 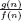 |