1.1 A Short Historical Perspective
The first step in Fluid Mechanics was certainly carried out by Archimedes ! ( 287, 212) who was a mathematician and a physicist in Antiquity. He formulated a now well-known theorem which says that a body immersed in a fluid supports an upward push equal to the weight of the displaced fluid. This is the first result in the theory of fluid equilibria. Knowledge did not evolve much until the works of Evangelista Torricelli (16081647) and Blaise Pascal (16231662). Torricelli did a famous experiment when he put upside down a tube full of mercury. The liquid went down a little and left a column of mercury 76cm high. Hence, it was demonstrated the existence of atmospheric pressure, the weight of air and the existence of vacuum, much discussed at the time. Pascal gave a full account of all these phenomena in his treatise Lquilibre des liqueurs published in 1663. The static of fluids was almost set up. Fluid dynamics started with the work of Leonhard Euler (17071783) who formulated for the first time the equation of motion of an inviscid fluid. Daniel Bernoulli (17001782) contributed to the study of such fluids with theorems on energy conservation that revealed fundamental properties of fluid flows. ! !
The next important step has been the formulation of the effects of viscosity. This was done during the nineteenth century with the work of Henri Navier (17851836), Georges Stokes (18191904) and Jean-Louis-Marie Poiseuille (17991869). Let us note that Isaac Newton (16421727) already showed the existence of viscosity with experiments and left his name associated with a kind of fluids (the most common ones like air and water) now known as the Newtonian fluids. NavierStokes equation, which controls the dynamics of viscous fluids, was first formulated by Navier in the case of a fluid with constant viscosity.
Then, fluid mechanics took various ways. We shall mention only the main ones. Studies of flows stability started with the works of Helmholtz (1868) and Lord Kelvin (1880). Heat transport was studied by W. Prout (1834), Rumford (1870), A. Oberbeck (1879), H. Bnard (1900), J. Boussinesq (1903) and Lord Rayleigh (1916). Turbulence focused the interest of O. Reynolds (1883), L. Prandtl (1920), A. Kolmogorov (1940), etc.
Presently, fluid dynamics is even more diversified, but some old problems resist: turbulence remains one of the main unsolved problem of classical physics.
1.2 The Concept of a Fluid
1.2.1 Introduction
Fluids gather a very large number of forms of matter which, as far as the most common are concerned (liquids and gases), can be characterized by the ease with which one can deform them. This point of view expresses the difference between the solid state and the fluid state which are both mechanical states. Common experience assumes that such a difference is obvious, however we shall see that a more detailed inspection somehow blurs the difference between solids and fluids. In fact, this difference is contained in a law, known as the rheological law, which states how the matter reacts to (is deformed by) a stress (a force per surface unit). Generally speaking, matter is considered as fluid if the internal (shear) stresses only depend on velocity gradients.
We shall come back on these concepts, but let us give a simple example to appreciate what is behind this definition. We consider a cork floating on water in a container. The cork is in A and we wish to move it to B. Because water is a fluid, the force we need to apply on the cork just depends on velocity gradients. It can be made as small as we wish; we just need to move the cork more slowly.
From the point of view of thermodynamics, we may say that the states A and B and cannot be distinguished: the energy and entropy variations needed to make the system passing from one state to the other can be made vanishingly small. On the contrary, if we did a similar experiment of a solid, some work would have been needed and the energy of the states A and B would differ.
1.2.2 Continuous Media
To describe the motion of a fluid, obviously we cannot (and do not wish to!) describe the motion of all its molecules or atoms individually. We are only interested in their mean motion. This means replacing the set of atoms or molecules which constitutes the fluid by a medium that behaves as this mean motion. Such an assumption is valid when the scale L , which we are interested in, is large compared to the mean free path of atoms or molecules. The ensuing approximation is measured by the Knudsen number
which needs to be small compared to unity. The cases where Kn1 is the subject of the dynamics of rarefied gases based on the kinetic theory of gases. In general, it is not included in fluid mechanics. An introduction to the relation between fluid dynamics and gas kinetics is given in Chap.
Thermodynamics and the dynamics of continuous media share many similarities in their description of matter. Indeed, in these two approaches, the microscopic components of matter are ignored and only mean values are retained. The drawback of such a way of doing is that some quantities can only be obtained by experiments, like heat capacity in thermodynamics or viscosity in fluid mechanics, the equation of state in thermodynamics or the rheological law in fluid mechanics. Their theoretical determination needs a more detailed approach based on the statistical properties of the microscopic components of matter (see Chap.).
1.3 Fluid Kinematics
The first step needed to understand the motion of fluids is to find the right tools that will allow us to describe a fluid flow. This is the role of fluid kinematics that study fluid motion without worrying about its causes.
1.3.1 The Concept of Fluid Particle
Very often, we shall use the concept of fluid particle or fluid element . This is an idealized view of a piece of fluid: it is so small that fluid properties are uniform inside. However, it is big enough so as to contain a large number of atoms or molecules, allowing us to assume that the fluid is locally in thermodynamic equilibrium (hence the temperature is defined). Such a particle is not a point mass: it owns a surface which authorizes contact forces with other particles.
1.3.2 The Lagrangian View
A first way for describing the fluid motion is to give the trajectories of all the fluid particles. Such a description is the Lagrangian one. It may be summarized by the set of trajectories of all fluid particles that were in the domain
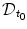
at t = t 0. Mathematically, it is the set
Such a description is used in some specific studies where it provides simplifications. However, generally speaking, its use is not very popular because of some intrinsic difficulties in the expression of stresses. We refer the reader to the end of this chapter for a more detailed presentation.
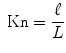
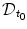 at t = t 0. Mathematically, it is the set
at t = t 0. Mathematically, it is the set