Andrea Pascucci and Wolfgang J. Runggaldier Unitext Financial Mathematics Theory and Problems for Multi-period Models 10.1007/978-88-470-2538-7_1 Springer-Verlag Italia 2012
1. Pricing and hedging
Abstract
In this chapter we introduce some of the basic ideas of the modern mathematical finance that will be used throughout the book. These are the concepts of risky and non-risky securities, primary assets and derivatives, including options, self-financing investment strategies and their portfolios. We also introduce the notion of arbitrage, the concept of equivalent martingale measure (EMM) and of a complete market. The issues covered in this chapter are basic problems of modern mathematical finance, i.e. the pricing and hedging of derivatives. To define the price of a derivative, which is not already traded on the market, we shall use one of the most common criteria namely the noarbitrage principle. According to this principle, in a market in equilibrium, prices of various securities are such that it is not possible to make a profit without risk by investing in the market by a self-financing strategy.
In this chapter we introduce some of the basic ideas of the modern mathematical finance that will be used throughout the book. These are the concepts of risky and non-risky securities, primary assets and derivatives, including options, self-financing investment strategies and their portfolios. We also introduce the notion of arbitrage, the concept of equivalent martingale measure (EMM) and of a complete market. The issues covered in this chapter are basic problems of modern mathematical finance, i.e. the pricing and hedging of derivatives. To define the price of a derivative, which is not already traded on the market, we shall use one of the most common criteria namely the no-arbitrage principle. According to this principle, in a market in equilibrium, prices of various securities are such that it is not possible to make a profit without risk by investing in the market by a self-financing strategy.
We then describe two typical examples of discrete-time market models with a single risky asset: the binomial model that is a complete market model and the trinomial model that is an example of an incomplete market model. This last model can be completed by adding a second risky asset and this will constitute another example of complete market. These three market models will be the basis for all exercises discussed in the book. We also remark that, for a finite time horizon, these models can be naturally defined on a finite probability space , as we assume throughout this book.
In a complete market any derivative can be replicated by a portfolio resulting from a self-financing investment strategy: furthermore, the prices of the various securities are uniquely determined by imposing the condition of absence of arbitrage opportunities. We shall also briefly discuss possible approaches to pricing and hedging in an incomplete market.
At last, using an alternative representation of the price of one of the basic options, that is the European Call option, we shall mention the so-called change of numeraire technique that is very useful in solving various problems in mathematical finance and in this book will be applied in Chapter 4 .
The exercises will focus on the evaluation and hedging of various types of derivatives, especially options. The last two exercises are an example of application of the techniques mentioned for the pricing and hedging in an incomplete market. For their solution, we apply a dynamic optimization methodology that will be studied in detail in Chapter 2 .
For this chapter we have relied primarily on []. Since these are very basic topics, they are treated in almost all introductory books on mathematical finance: among those listed in the bibliography we mention here [], [], [], [], [], [], [].
1.1 Primary securities and strategies
1.1.1 Discrete time markets
Consider a probability space (, , P )where has a finite number of elements and where we assume that is the power set of with P ({}) > 0 for any . We let t 0, t 1, ..., t N with
represent the trading dates: to fix the ideas, t 0 = 0 denotes todays date and t N = T the expiry date of a derivative.
A discrete time market model consists of a non-risky asset (bond) B and a certain number of risky assets (stocks) S 1, ..., S d , with d . The bond has the following deterministic dynamics: if B n denotes the value of the bond at time t n , we have
where r n > 1 denotes the risk-free rate in the n -th period[ t n 1, t n ]. Occasionally we will refer to this asset as the bank account .
The risky securities have the following stochastic dynamics: if S n i denotes the price at time t n of the i -th asset, then we have
where n i is a real random variable that represents the rate of return of the i -th asset in the n -th period[t n 1, t n ].
We set
and suppose that the process n is adapted to a generic filtration ( n ) with 0 = {
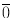
, }. Since in the market models considered in this book, based on (), the sequence n will be the only source of randomness, we assume n generated by n , that is
Finally, since () establishes a bijective correspondence between the processes n and S n , the filtration ( n ) coincides with the filtration generated by S , that is
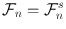
for any n . In more general situations, however, we will typically have
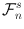
n and occasionally, as later in the definition of derivatives, also in this book we will use the notation
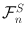
when we want to emphasize that the filtration considered is the one generated by the underlying asset prices S . However in this book we will always have
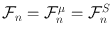
and this -algebra represents the market information available at time t n . We also assume that n is independent on n 1 for any n =1,, N .
Notice that as elements of the basic probability space we can take the various realizations of the sequence n . Therefore if n assumes a finite number of values, as in the binomial (cf. ) market models, then the set contains a finite number of elements as we had supposed.

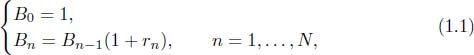
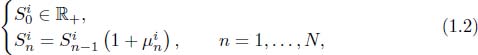
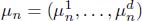
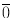 , }. Since in the market models considered in this book, based on (), the sequence n will be the only source of randomness, we assume n generated by n , that is
, }. Since in the market models considered in this book, based on (), the sequence n will be the only source of randomness, we assume n generated by n , that is 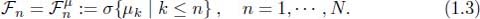
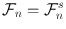 for any n . In more general situations, however, we will typically have
for any n . In more general situations, however, we will typically have 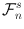 n and occasionally, as later in the definition of derivatives, also in this book we will use the notation
n and occasionally, as later in the definition of derivatives, also in this book we will use the notation 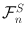 when we want to emphasize that the filtration considered is the one generated by the underlying asset prices S . However in this book we will always have
when we want to emphasize that the filtration considered is the one generated by the underlying asset prices S . However in this book we will always have 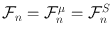 and this -algebra represents the market information available at time t n . We also assume that n is independent on n 1 for any n =1,, N .
and this -algebra represents the market information available at time t n . We also assume that n is independent on n 1 for any n =1,, N .












