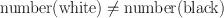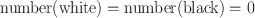Derrick G. Kourie - The Correctness-by-Construction Approach to Programming

The Correctness-by-Construction Approach to Programming — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "The Correctness-by-Construction Approach to Programming" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...95

Derrick G. Kourie and Bruce W. Watson The Correctness-by-Construction Approach to Programming 2012 10.1007/978-3-642-27919-5_1 Springer-Verlag Berlin Heidelberg 2012

1. Introduction

Derrick G. Kourie 1 and Bruce W. Watson 2

(1)

Department of Computer Science, University of Pretoria, Pretoria, South Africa

(2)

FASTAR Group, Information Science, Stellenbosch University, Stellenbosch, South Africa

Abstract

There are many debates amongst software engineers about the extent to which one should engage in so-called upfront design. But the focus of the debate relates mostly to programming-in-the-large: how to approach the problem of designing a large system of interacting objects or components.

There are many debates amongst software engineers about the extent to which one should engage in so-called upfront design. But the focus of the debate relates mostly to programming-in-the-large: how to approach the problem of designing a large system of interacting objects or components. The Big Upfront Design (BUD) adherents believe that energy should go into developing an initial overall architectural outline of the system; the adherents of the more recent agile software development movement are inclined to let a system architecture evolve from the bottom up, so to speak. Their energy goes into identifying small components of the overall system, developing test cases and writing code that handles these test cases.

But whatever view one takes, it seems thatas a matter of factby the time people get down to programming-in-the-small (i.e. actually writing code), there is rapid recourse to the keyboard:

Try a little bit of this and a little bit of that; put in an if-command here and a loop there; two int variables would seem to do the trick; let us try to compile; oopsforgot about the else part of the if-command; compile again; oh deara syntax error; fix and recompile; run the test cases; darntest case 3 fails; desperately resort to pen and paper to scratch out a couple of exploratory diagrams; ahperhaps a separate method is needed to deal with a newly-discovered boundary condition

Those who do not recognise this kind of scenario are truly blessed. To most real programmers, it will be painfully, if not embarrassingly, familiar. The purpose of these notes is to change the way that readers think when coding at this programming-in-the-small level.

Now we are not so nave as to believe that we will persuade all and sundry to derive paper solutions to problems before entering code at a keyboard. It is just as vain to hope that the multitudes will take time to sit cross-legged in Zen-like meditation to clearly think through the problem at hand before taking to a keyboard, desirable as such a practice may be! However, we do cherish a fond hope that this book will change thought processes: that they will foster the kind of mentality that, almost as a matter of second nature, asks: what should the pre- and postconditions be for this method; what holds at the end of this piece of code; what might be the loops invariant, etc. And we will not be disappointed if a few individuals discover that it is sometimes actually both intellectually pleasing and time-wise profitable to derive a paper solution to critical problems in the code, before hitting the keyboard.

The underlying problem solving strategy that we advocate is to refine progressively an abstract description of a problemits specification in terms of pre- and postconditionsto its ever-more concrete realisation, culminating in the concrete solution specified in Guarded Command Language (GCL). A very particular kind of abstract specification is one in which the pre- and postcondition is invariant by which we roughly mean that they are the same, barring certain variations in the variable values that describe them. It will be seen that such invariance is an extremely powerful aid to solving iterative problems. Invariance lies at the heart of the solution to practically all the example problems that we will later be considering. Because of its importance, and to sharpen intuition, we now present two example problems that are easily solved by identifying invariants.

1.1 Invariance Examples

An invariant of a sequence of steps to solve a problem, is a condition that is true before carrying out those steps, and that remains true after executing the entire sequence of steps. If the problem solution is somehow made easier as a result of executing the sequence once, then one would hope that by repeatedly executing the sequence of steps (i.e. by looping) the problem can eventually be solved. It is important to note that the invariant is not required to hold after each step; rather, it should hold after executing the entire sequence.

The following two problems serve as a foretaste of the kind of thinking that will be promoted in the remainder of this text. They show that the notion of an invariant of a sequence of steps can be a powerful aid to solving problems.

1.1.1 A Chess Board Problem

Consider an 8 8 chess board from which the squares in the upper left and lower right corners have been removed, as shown in Fig.. Also available is a large number of domino tiles such as the two shown to the right of the board in the figure, each of which covers exactly two squares of the chess board. Assume that tiles may not lie on top of one another. Nor may they hang over the edge of the chess board.

Fig. 1.1

Chessboard and squares

Is it possible to lay tiles on the chess board in such a way so that all squares are covered?

If you try an exhaustive approach to laying all combinations of domino tiles on the board, you might eventually arrive at an answer. This is the equivalent of trying to hack out an answer to a coding problem on a trial-and-error basis at a keyboard. However, there is a more subtle and elegant way to tackle the problem. Consider the following assertions:

• A regular chess board contains the same number of black and white squares.
• The modified chess board in this problem has had two white squares removedtherefore it has two more black than white squares.
• Every tile placement reduces by one the number of uncovered black squares and the number of uncovered white squares.
• Thus, no matter how one lays a tile, there will always be more black squares than white squares.
  One could express this by saying that the following relationship is invariant with respect to the tile laying operation:

  
• As a consequence, there is no way of laying the tiles so that

  

Becoming aware of an invariant in this problem space not only rapidly leads to an answer to the problem; it also indicates solutions to a whole class of similar problems. The chess board did not have to be the standard 8 8 size: it could have had an arbitrary number of columns and rows. Neither was it necessary to couch the problem in terms of removing two squares from opposite corners: any number of squares could have been removed from anywhere on the board. The answer to the problem would have been the same, for any starting position such that number(white)number(black).

Next page

1234567...95

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «The Correctness-by-Construction Approach to Programming»

Look at similar books to The Correctness-by-Construction Approach to Programming. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Derrick mwiti

Deep learning with TensorFlow and Keras

Belmont and Belcourt Biographies

Derrick Rose: An Unauthorized Biography

Derrick Jaxn

Ive Come Too Far

John Sauer

Constitutional Correctness Trumps Political Correctness

Derrick Jensen

Bright Green Lies

Spires Derrick R.

The Practice of Citizenship

Derrick Rose

Ill Show You

Sarah Derrick

A No-Fluff Guide To Homemade DISINFECTANT SPRAY A Simple Approach to making bleach and alcohol-based wipes and spray

Derrick Jensen

The Culture of Make Believe

Derrick Chambers

Kidney Friendly Recipes

Derrick Levasseur

The Undercover Edge

Richard Delgado

The Derrick Bell Reader

Discussion, reviews of the book The Correctness-by-Construction Approach to Programming and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.