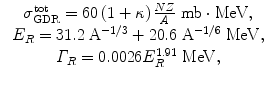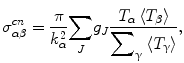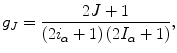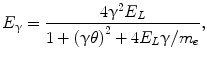Nakajima - Nuclear Back-end and Transmutation Technology for Waste Disposal: Beyond the Fukushima Accident

Nuclear Back-end and Transmutation Technology for Waste Disposal: Beyond the Fukushima Accident — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Nuclear Back-end and Transmutation Technology for Waste Disposal: Beyond the Fukushima Accident" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...81

Part I
Basic Research for Nuclear Transmutation and Disposal: Physical and Chemical Studies Relevant to Nuclear Transmutation and Disposal Such as Measurement or Evaluation of Nuclear Cross-Section Data

The Author(s) 2015

Ken Nakajima (ed.) Nuclear Back-end and Transmutation Technology for Waste Disposal 10.1007/978-4-431-55111-9_1

1. Nuclear Transmutation of Long-Lived Nuclides with Laser Compton Scattering: Quantitative Analysis by Theoretical Approach

Shizuka Takai 1 and Kouichi Hagino 2

(1)

Nuclear Safety Research Center, Japan Atomic Energy Agency, Tokai-mura, Naka-gun Ibaraki, 319-1115, Japan

(2)

Department of Physics, Tohoku University, Sendai Miyagi, 980-8578, Japan

Shizuka Takai

Email:

Abstract

A photo-neutron (,n) reaction with laser Compton scattering -rays has been suggested to be effective for the nuclear transmutations of fission products. The photo-neutron reaction occurs via a giant dipole resonance, which has a large cross section and whose properties are smooth functions of mass number. The laser Compton scattering can generate effectively and selectively high-energy photons with a desired energy range. In this chapter, we investigate quantitatively the effectiveness of the transmutation with laser Compton scattering based on the HauserFeshbach theory using the TALYS code. We carry out simulations for high-decay heating nuclide 137Cs, in which the cross sections for 137Cs (,), (,n), and (,2n) reactions, and the total photonuclear reaction cross sections versus incident photon energy, are calculated. The incident photon energy obtained by laser Compton scattering is also optimized. It is shown that the transmutation with medium-energy photon with a flux of more than 1018/s effectively reduces the radioactivity of the target 137Cs.

Keywords

137Cs Giant dipole resonance Laser Compton scattering Photo-neutron reaction Radioactive wastes Transmutation

1.1 Introduction

One of the major problems of the nuclear fuel cycle is the disposal of high-level radioactive waste that contains long-lived nuclides such as 129I and high-decay heating nuclides such as 137Cs. After the severe accident at the Fukushima Daiichi Nuclear Power Plant, there is also a problem of 137Cs having been concentrated by treatment of contaminated water. Transmuting such nuclides into short-lived or stable nuclides is one possible way to resolve this problem. Neutron capture reactions have been proposed for transmutations of such fission products. However, the neutron capture cross sections differ significantly from nuclide to nuclide, and this transmutation method is not effective for nuclides with small neutron capture cross sections such as 137Cs.

Recently, photo-neutron (,n) reactions with laser Compton scattering -rays have been suggested as an alternative method for nuclear transmutations [], which has a large cross section for most nuclides. The GDR is a collective excitation of a nucleus that decays mainly by the emission of neutrons, and its total cross section is a smooth function of mass number. Therefore, this method is expected to be effective for transmuting fission products regardless of isotopes.

Fig. 1.1

Schematic illustration of nuclear transmutation with laser Compton scattering

So far, transmutation with laser Compton scattering for some nuclides has been evaluated only in a simple manner. In this chapter, we investigate more quantitatively the effectiveness of the transmutation with laser Compton scattering, especially for 137Cs.

1.2 Calculation Method

1.2.1 Reaction via Giant Dipole Resonance

Nuclear transmutation with laser Compton scattering uses photonuclear reactions via GDR because the cross section of GDR is quite large and the total cross section is a smooth function of mass number. GDR is a collective excitation of a nucleus involving almost all nucleons, which is interpreted classically as a macroscopic oscillation of a bulk of protons against that of neutrons. The total cross section GDRtot, the resonance energy E R , and the width R are given by []

(1.1)

where N and Z are the neutron and proton numbers, A = N + Z is the mass number, and , which is roughly equal to 0.2 for medium nuclides, is a correction coefficient for the pion exchange.

When a target nucleus is irradiated with a photon and excited to GDR, it often forms a compound nucleus with only a small contribution of a pre-equilibrium reaction []. The compound nucleus is an excited state in which the energy brought by the incident particle is shared among all degrees of freedom of the nucleus. The reaction cross section from an initial channel to a final channel proceeding through a compound nucleus state of spin J can be written by the HauserFeshbach formula as

(1.2)

where k is the wave number in the initial channel, g J is a statistical factor, T is a transmission coefficient, and T is the energy average of T . The statistical factor is

(1.3)

where i and I are the projectile and target spins.

Calculations of reaction cross sections are performed using the nuclear model code TALYS (version 1.4) [].

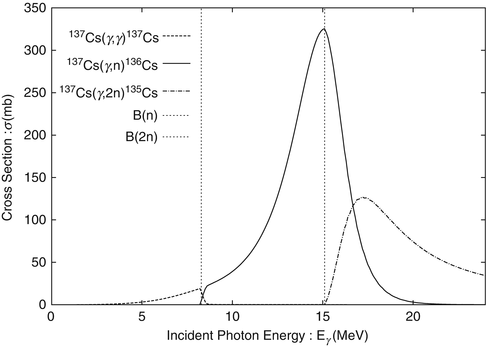
Figure shows the photonuclear reaction cross sections of 137Cs calculated using the TALYS code. In the incident photon energy B (n) E < B (2n), where B (n) and B (2n) are the one- and two-neutron binding energies, respectively, we can see that the (,n) reaction mainly occurs. Because the resonance energy of GDR E R is 1518 MeV, which is roughly equal to B (2n) for medium nuclides, about half the reactions via GDR are (,n) reactions, which occur at B (n) E < B (2n).

Fig. 1.2

Cross sections for 137Cs (,), 137Cs ( dashed line ), 137Cs (,n), 136Cs ( solid line ), and 137Cs (,2n). 135Cs ( dash-dot line ) reactions versus incident photon energy: dotted lines represent B (n) and B (2n) of 137Cs

1.2.2 High-Energy Photons Obtained by Laser Compton Scattering

Laser Compton scattering is a method to obtain high-energy photons by laser photons backscattered off energetic GeV electrons. In the case of head-on collision between relativistic electrons and laser photons, the energy of scattered photons is given by

(1.4)

where = E e / m e is the Lorentz factor of the electron beam with energy E e , m e is the rest mass of the electron, E L is the energy of the laser photon, and is the scattering angle. From Eq. (), the energy of the scattered photon is maximum at =0, and it depends on the energy of incident electrons and photons. The minimum energy of the scattered photon can be fixed by controlling with collimators.

Next page

1234567...81

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Nuclear Back-end and Transmutation Technology for Waste Disposal: Beyond the Fukushima Accident»

Look at similar books to Nuclear Back-end and Transmutation Technology for Waste Disposal: Beyond the Fukushima Accident. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Giulia de Togni

Fall-out from Fukushima: Nuclear Evacuees Seeking Compensation and Legal Protection After the Triple Meltdown

Danielle Smith-Llera

Fukushima Disaster: How a Tsunami Unleashed Nuclear Destruction

Richard Hindmarsh

Nuclear Disaster at Fukushima Daiichi: Social, Political and Environmental Issues

Naoto Kan

The Fukushima Nuclear Power Plant Disaster and the Future of Renewable Energy

Thomas R. Wellock

Safe Enough?: A History of Nuclear Power and Accident Risk

Deirdre Langeland

Meltdown: Earthquake, Tsunami, and Nuclear Disaster in Fukushima

Nakajima Hikōki Kabushiki Kaisha.

Nakajima B5N Kate and B6N Jill Units

Joonhong Ahn Cathryn Carson Mikael Jensen Kohta Juraku

Reflections on the Fukushima Daiichi Nuclear Accident

Casto

Station blackout: inside the Fukushima nuclear disaster and recovery

Charles A. Casto

Station Blackout: Inside the Fukushima Nuclear Disaster and Recovery

Fred Pearce

Fallout: Disasters, Lies, and the Legacy of the Nuclear Age

David Lochbaum

Fukushima: The Story of a Nuclear Disaster

Discussion, reviews of the book Nuclear Back-end and Transmutation Technology for Waste Disposal: Beyond the Fukushima Accident and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.