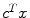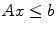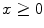1. Linear Programming
1.1 Introduction
Operations research employs the scientific method as a basis to deal with decision-making problems by designing and solving mathematical models. One of the most studied and developed is linear programming, which seeks to optimise a linear objective function that is subject to some constraints which are also linear. The name linear programming does not come from producing computer programmes, but originates from planning activities carried out in an organization to optimise available resources.
Linear programming techniques are employed in a large number of problems, such as production planning, financial planning, human resources management, transport problems, distribution, allowances designs, forest planning, scheduling flights, etc. It is also worth stressing the significant progress made by optimization software due to the increased calculation power of computers and to the fall in hardware costs. There is a considerable number of software packages available to solve linear programming problems.
The basis of linear programming lies in the study of linear inequalities, which appeared for the first time in the work of Fourier (17681830). Kantorovich () also contemplated the linear problem to obtain a suitable diet at a minimum cost based on 77 foods by considering nine nutrients. This problem acknowledged the structure of optimising a linear function subject to linear constraints.
Linear programming really began to arouse interest as from 1947 when Dantzig () in the United States.
Koopmans () to solve production planning problems by employing transport methods.
In 1975, Kantorovich received the Nobel Prize in Economics from the Royal Swedish Academy of Sciences for his contributions to the optimum resources allocation problem. He shared this prize with Tjalling Charles Koopmans. Apparently, the Academy considered that Dantzigs work was too mathematical and there is no Nobel Prize in Mathematics.
Linear programming is a mathematical process to determine the optimum allocation of scarce resources. Allocation problems can come in widely varying forms. There are two types of very common problems: the product mix problem and the mixtures problem. The product mix problem intends to discover which and how many products must be included in the production programme to maximise profits. The mixtures problem attempts to determine the minimum quantity of resources possible to be used to obtain a given level of product or service. Any linear programming problem consists in an objective function and a set of constraints which must satisfy the following conditions: the objective function must be linear; the objective must represent the decision makers goal and must be the maximisation or the minimization of a linear function; constraints must also be linear.
There are two important object types for most linear programming problems: first, limited resources and second, activities. Each activity consumes or provides additional quantities of resources. The problem consists in determining the best combination of levels of the activities that do not employ more resources than those available. The Simplex Method is a widely used solution algorithm for solving linear programmes. The graphic method is useful when there are only two decision variables.
Linear programming models offer a series of limitations owing to some assumptions created to simplify reality and to represent it by means of a mathematical model. The created assumptions are:
Deterministic problems are considered. In other words, all the data are known with certainty.
It is assumed that the objective function is linear.
Constraints are also considered linear.
Decision variables cannot take negative values.
The additivity of resources, the total use of each resource, is obtained by summing partial usages of this resource.
The divisibility of decision variables; these variables can take fractional values.
Independency is assumed among activities and resources for the various decision variables.
Both the quantity of the resource employed and the objective function value are proportional to the values of the decision variables. This proportionality requirement is met as the function is objective and constraints are linear.
A linear programming model consists of the following components: decision variables, objective function and constraints. These three model components are linked by mathematical relations.
Decision variables are those factors among which the decision maker must choose and they are controllable variables. The aim of linear programming is to find the best values for these decision variables. In linear programming, variables may take fractional values. In a decision-making process, some factors affect the result variables, but they are not controllable by the decision maker. These input parameters represent the limitations imposed by the environment (interest rates, prices of raw materials, market demand, etc.). The objective function represents the relation between decision variables and uncontrollable variables. The objective could be the maximisation or minimization of any quantity, and is limited by constraints. Constraints express the limitations imposed on management systems owing to the relations with the environment.
Building a linear programming model consists in the following steps: (1) defining decision variables; (2) defining the objective or goal in terms of the decision variables; (3) defining all the system constraints and (4) restricting all the variables so they are not negative. A linear programming model can be expressed canonically as:
where x represents the vector of decision variables, c and b are vectors of known coefficients and A is a known matrix of coefficients. Objective function cx can be maximised or minimised. Inequalities Ax b are the constraints. The non-negativity constraint is represented by x 0.