1.1 Background
Reynolds (), it is called the boundary layer transition.
For over a century, fluid dynamics researchers have devoted a vast amount of efforts in understanding this fundamental phenomenon, and have developed various theories and analytical or numerical methods to describe it. This is not only because the transition problem is in nature a turbulence problem, a century-old research topic in fluid dynamics, but also because of its prime importance in the design of advanced aircraft, ships, submarines, jet propulsions and more. The laminar and turbulent boundary layers, two common fluid states in natural environments, have rather different aerodynamic and heat transfer characteristics. Engineers have utilized the flow transition phenomenon for boundary layer control in order to improve the aerodynamic and thermal performance of the vehicle in interest. It is desired to maintain a large laminar boundary layer on a vehicle surface in order to reduce the overall drag. This is due to significantly lower skin frictions of the laminar boundary layer comparing to a turbulent boundary layer at the same Reynolds number. In addition, the effects of heat transfer are crucial for the safe operation and lifespan of reentry vehicles and gas turbine blades in jet propulsion systems. Because the rate of heat transfer is much higher in the turbulent boundary layer than in the laminar boundary layer counterpart, it calls for a thermal management strategy using transition and flow control techniques. Contrarily, there are situations that the turbulent boundary layer is preferred, due to its better resistance to adverse pressure gradients and flow separations than the laminar boundary layer. Laminar flow is often triggered into turbulent flow prematurely in order to prevent or postpone flow separations, or improve the mixing effect and the burning efficiency of combustors in gas turbine systems.
As the boundary layer transition and flow control are highly relevant to engineering designs and applications in various industries, investigations of transition phenomena are often carried out through wind tunnel tests, theoretical analyses, computational modeling and simulations, or a combination of these methods. Sometimes flight tests may be required to verify a flow control approach or an analytical and numerical prediction. In the following sections, three common transition modes are described, followed by several common flow parameters that may influence the transition onset and process.
1.2 Transition Modes
The viscous flow transition can occur in many occasions such as boundary layer flows, shear flows and Poiseulli flows. However, the transition occurred within the boundary layer is the most complicated one and of prime importance to engineering designs such as aircraft, ships, cars, and jet propulsion systems. Because the boundary layer transition process can be triggered by different mechanisms in various applications, it is important to identify different transition modes in order to obtain basic understanding of the underlying physics.
1.2.1 Natural Transition
Natural transition, also commonly called normal transition, typically occurs in an environment with weak background noise or free-stream turbulence level ( Tu ). This transition is characterized by the formation of two-dimensional Tollminen-Schlichting (T-S) waves (Tollminen ).
Natural transition process in boundary layers can be divided into two stages. The first stage is the reception of disturbance waves from the free-stream or rough surface, which is denoted receptivity (Saric et al. ).
1.2.2 Bypass Transition
Klebanoff et al. ().
Bypass transition is the most common transition mode in engineering applications, and is of practical importance as it signifies the departure of the skin friction from the laminar flow value. Good examples of bypass transition would be multi-stage turbine blades periodically impinged by passing wakes (Wu et al..
1.2.3 Separation-Induced Transition
Separation-induced transition occurs when a laminar separation bubble forms at the leading edge of an airfoil due to adverse pressure gradients or large surface curvatures, and reattaches as turbulent flow in the downstream on the airfoil. Depending on the pressure distribution around the airfoil and other factors such as the free-stream turbulence, the laminar separation bubble can have different lengths (Mayle ), which have a significant impact on the lift and drag characteristics of the device. A short separation bubble on the airfoil triggers the laminar flow into turbulent due to inherently unsteady nature of laminar flows. A long separation bubble, however, can cause a thick boundary layer downstream or even lead to massive flow separation or stall on the airfoil.
Measurements of separation-induced transition are relatively easy to carry out in fixed or two-dimensional airfoils, but are more challenging in three-dimensional rotary rotors. Wadcock and Yamauchi ().
1.2.4 Reverse Transition
Reverse transition is also called relaminarization where turbulent flow is reversed back to a laminar state. This can occur when a flow acceleration parameter,
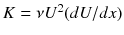
, reaches a level of 3.2 106 or higher (Mayle ) over a flat plat with a free-stream turbulent intensity of 0.1 %, which shows the relamonarization followed by a retransition process.
1.3 Transition Parameters
It has been recognized that several flow and geometric parameters may influence the transition process. It is important to note that a transition process is often triggered by combined effects of different factors, whose influence can vary in different situations. Therefore, it would be beneficial to understand how these parameters influence the transition onset and process. This would not only help scientists develop enhanced theories and models to describe the transition phenomena, but also engineers designing optimal flow control strategies in practical engineering applications.
1.3.1 Free-Stream Turbulence
The free-stream turbulence level ( Tu ) is known to have a large influence on all transition modes. A high level of the free-stream turbulence often triggers bypass transitions, which are the most common transition modes in engineering applications. It also influences separation-induced transitions, and sometimes determines whether or not a laminar separation bubble will reattach as turbulent flow or burst into massive separation. Numerical investigations indicated that the influence of free-stream turbulence on the transition onset is weakened under strong pressure gradients, as demonstrated in the numerical computations for highly twisted proprotors by Sheng and Zhao ().









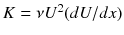 , reaches a level of 3.2 106 or higher (Mayle ) over a flat plat with a free-stream turbulent intensity of 0.1 %, which shows the relamonarization followed by a retransition process.
, reaches a level of 3.2 106 or higher (Mayle ) over a flat plat with a free-stream turbulent intensity of 0.1 %, which shows the relamonarization followed by a retransition process.