SpringerBriefs in Philosophy
SpringerBriefs present concise summaries of cutting-edge research and practical applications across a wide spectrum of fields. Featuring compact volumes of 50 to 125 pages, the series covers a range of content from professional to academic. Typical topics might include:
A timely report of state-of-the art analytical techniques
A bridge between new research results, as published in journal articles, and a contextual literature review
A snapshot of a hot or emerging topic
An in-depth case study or clinical example
A presentation of core concepts that students must understand in order to make independent contributions
SpringerBriefs in Philosophy cover a broad range of philosophical fields including: Philosophy of Science, Logic, Non-Western Thinking and Western Philosophy. We also consider biographies, full or partial, of key thinkers and pioneers.
SpringerBriefs are characterized by fast, global electronic dissemination, standard publishing contracts, standardized manuscript preparation and formatting guidelines, and expedited production schedules. Both solicited and unsolicited manuscripts are considered for publication in the SpringerBriefs in Philosophy series. Potential authors are warmly invited to complete and submit the Briefs Author Proposal form. All projects will be submitted to editorial review by external advisors.
SpringerBriefs are characterized by expedited production schedules with the aim for publication 8 to 12 weeks after acceptance and fast, global electronic dissemination through our online platform SpringerLink. The standard concise author contracts guarantee that
an individual ISBN is assigned to each manuscript
each manuscript is copyrighted in the name of the author
the author retains the right to post the pre-publication version on his/her website or that of his/her institution.
More information about this series at http://www.springer.com/series/10082
David Ellerman
New Foundations for Information Theory
Logical Entropy and Shannon Entropy
1st ed. 2021
Logo of the publisher
David Ellerman
Faculty of Social Sciences, University of Ljubljana, Ljubljana, Slovenia
ISSN 2211-4548 e-ISSN 2211-4556
SpringerBriefs in Philosophy
ISBN 978-3-030-86551-1 e-ISBN 978-3-030-86552-8
https://doi.org/10.1007/978-3-030-86552-8
Mathematics Subject Classication (2010): 03A05 94A17
SpringerBriefs in Philosophy
The Author(s), under exclusive license to Springer Nature Switzerland AG 2021
This work is subject to copyright. All rights are solely and exclusively licensed by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.
The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.
The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, expressed or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This Springer imprint is published by the registered company Springer Nature Switzerland AG
The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland
To the memory of Gian-Carlo Rotamathematician, philosopher, mentor, and friend.
About this book
This book presents a new foundation for information theory where the notion of information is defined in terms of distinctions, differences, distinguishability, and diversity. The direct measure is logical entropy which is the quantitative measure of the distinctions made by a partition. Shannon entropy is a transform or re-quantification of logical entropy that is especially suited for Claude Shannons mathematical theory of communications. The interpretation of the logical entropy of a partition is the two-draw probability of getting a distinction of the partition (a pair of elements distinguished by the partition) so it realizes a dictum of Gian-Carlo Rota: 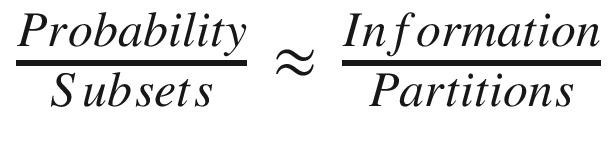 . Andrei Kolmogorov suggested that information should be defined independently of probability, so logical entropy is first defined in terms of the set of distinctions of a partition and then a probability measure on the set defines the quantitative version of logical entropy. We give a history of the logical entropy formula that goes back to Corrado Ginis 1912 index of mutability and has been rediscovered many times. In addition to being defined as a (probability) measure in the sense of measure theory (unlike Shannon entropy), logical entropy is always non-negative (unlike three-way Shannon mutual information) and finitely-valued for countable distributions. One perhaps surprising result is that in spite of decades of MaxEntropy efforts based maximizing Shannon entropy, the maximization of logical entropy gives a solution that is closer to the uniform distribution in terms of the usual (Euclidean) notion of distance. When generalized to metrical differences, the metrical logical entropy is just twice the variance, so it connects to the standard measure of variation in statistics. Finally, there is a semi-algorithmic procedure to generalize set-concepts to vector-space concepts. In this manner, logical entropy defined for set partitions is naturally extended to the quantum logical entropy of direct-sum decompositions in quantum mechanics. This provides a new approach to quantum information theory that directly measures the results of quantum measurement.
. Andrei Kolmogorov suggested that information should be defined independently of probability, so logical entropy is first defined in terms of the set of distinctions of a partition and then a probability measure on the set defines the quantitative version of logical entropy. We give a history of the logical entropy formula that goes back to Corrado Ginis 1912 index of mutability and has been rediscovered many times. In addition to being defined as a (probability) measure in the sense of measure theory (unlike Shannon entropy), logical entropy is always non-negative (unlike three-way Shannon mutual information) and finitely-valued for countable distributions. One perhaps surprising result is that in spite of decades of MaxEntropy efforts based maximizing Shannon entropy, the maximization of logical entropy gives a solution that is closer to the uniform distribution in terms of the usual (Euclidean) notion of distance. When generalized to metrical differences, the metrical logical entropy is just twice the variance, so it connects to the standard measure of variation in statistics. Finally, there is a semi-algorithmic procedure to generalize set-concepts to vector-space concepts. In this manner, logical entropy defined for set partitions is naturally extended to the quantum logical entropy of direct-sum decompositions in quantum mechanics. This provides a new approach to quantum information theory that directly measures the results of quantum measurement.
Acknowledgements
After Gian-Carlo Rotas untimely death in 1999, many of us who had worked or coauthored with him set about to develop parts of his unfinished work. My own work focused on developing his initial efforts on the logic of equivalence relations or partitions. Since the notion of a partition on a set is the category-theoretic dual to notion of a subset of a set, the first product was the logic of partitions (see the Appendix) that is dual to the Boolean logic of subsets (usually presented as propositional logic). Rota had additionally emphasized that the quantitative version of subset logic was logical probability theory and that probability is to subsets as information is to partitions. Hence the next thing to do in this Rota-suggested program was to develop the quantitative version of partition logic as a new approach to information theory. The topic of this book is this logical theory of information based on the notion of the logical entropy of a partitionthat then transforms in a uniform way to the well-known entropy formulas of Shannon. The book is dedicated to Rotas memory to acknowledge his influence on this whole project.
















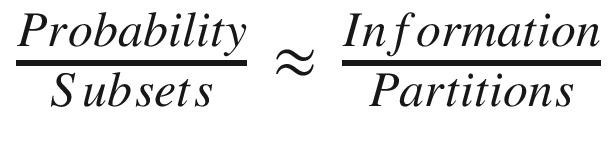 . Andrei Kolmogorov suggested that information should be defined independently of probability, so logical entropy is first defined in terms of the set of distinctions of a partition and then a probability measure on the set defines the quantitative version of logical entropy. We give a history of the logical entropy formula that goes back to Corrado Ginis 1912 index of mutability and has been rediscovered many times. In addition to being defined as a (probability) measure in the sense of measure theory (unlike Shannon entropy), logical entropy is always non-negative (unlike three-way Shannon mutual information) and finitely-valued for countable distributions. One perhaps surprising result is that in spite of decades of MaxEntropy efforts based maximizing Shannon entropy, the maximization of logical entropy gives a solution that is closer to the uniform distribution in terms of the usual (Euclidean) notion of distance. When generalized to metrical differences, the metrical logical entropy is just twice the variance, so it connects to the standard measure of variation in statistics. Finally, there is a semi-algorithmic procedure to generalize set-concepts to vector-space concepts. In this manner, logical entropy defined for set partitions is naturally extended to the quantum logical entropy of direct-sum decompositions in quantum mechanics. This provides a new approach to quantum information theory that directly measures the results of quantum measurement.
. Andrei Kolmogorov suggested that information should be defined independently of probability, so logical entropy is first defined in terms of the set of distinctions of a partition and then a probability measure on the set defines the quantitative version of logical entropy. We give a history of the logical entropy formula that goes back to Corrado Ginis 1912 index of mutability and has been rediscovered many times. In addition to being defined as a (probability) measure in the sense of measure theory (unlike Shannon entropy), logical entropy is always non-negative (unlike three-way Shannon mutual information) and finitely-valued for countable distributions. One perhaps surprising result is that in spite of decades of MaxEntropy efforts based maximizing Shannon entropy, the maximization of logical entropy gives a solution that is closer to the uniform distribution in terms of the usual (Euclidean) notion of distance. When generalized to metrical differences, the metrical logical entropy is just twice the variance, so it connects to the standard measure of variation in statistics. Finally, there is a semi-algorithmic procedure to generalize set-concepts to vector-space concepts. In this manner, logical entropy defined for set partitions is naturally extended to the quantum logical entropy of direct-sum decompositions in quantum mechanics. This provides a new approach to quantum information theory that directly measures the results of quantum measurement.