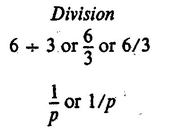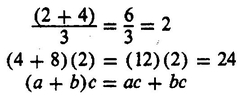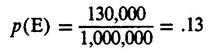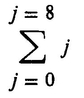APPENDIX:
On Mathematical Notation
THE READER WILL FIND a fairly liberal use of mathematical notation in this book, including a number of equations. This may incline him to say the book is full of mathematics.
Of course it is. Communication theory is a mathematical theory, and, as this book is an exposition of communication theory, it is bound to contain mathematics. The reader should not, however, confuse the mathematics with the notation used. The book could contain just as much mathematics and not include one symbol or equality sign.
The Babylonians and the Indians managed quite a lot of mathematics, including parts of algebra, without the aid of anything more than words and sentences. Mathematical notation came much later. Its purpose is to make mathematics easier, and it does for anyone who becomes familiar with it. It replaces long strings of words which would have to be used over and over again with simple signs. It provides convenient names for quantities that we talk about. It presents relations concisely and graphically to the eye, so that one can see at a glance the relations among quantities which would otherwise be strewn through sentences that the eye would be perplexed to comprehend as a whole.
The use of mathematical notation merely expresses or represents mathematics, just as letters represent words or notes represent music. Mathematical notation can represent nonsense or nothing, just as jumbled letters or jumbled notes can represent nothing. Crackpots often write tracts full of mathematical notation which stands for no mathematics at all.
In this book I have tried to put all the important ideas into words in sentences. But, because it is simpler and easier to understand things written concisely in mathematical notation, I have in most cases put statements into mathematical notation also. I have to a degree explained this throughout the book, but here I summarize and enlarge on these explanations. I have also ventured to include a few simple related matters which are not used elsewhere in this book, in the hope that these may be of some general use or interest to the reader.
The first thing to be noted is that letters can stand for numbers and for other things as well. Thus, in Chapter V, B j stands for a group or sequence of symbols or characters, a group of letters perhaps; j signifies which group. For the first group of letters, j might be 1, and that first group might be AAA, for instance. For another value of j , say, 121, the group of letters might be ZQE.
We often have occasion to add, subtract, multiply, or divide numbers. Sometimes we represent the numbers by letters. Examples of the notations for these operations are:
Addition
2 + 3
a + d
We read a + d as a plus d . We may interpret a + d as the sum of the number represented by a and the number represented by d .
Subtraction
5 4
q r
We read q r as q minus r .
Multiplication
3 5 or 3 : 5 or (3) (5)
u v or u v or uv
If we did not use parentheses to separate 3 and 5 in (3) (5), we would interpret the two digits as 35 (thirty-five). We can use parentheses to distinguish any quantities we want to multiply. We could write uv as ( u ) ( v ), but we dont need to. We read (3) (5) as 3 times 5, but we read uv as uv with no pause between the u and v , rather than as u times v .
We ordinarily read 1/ p as 1 over p rather than as 1 divided by p .
Quantities included in parentheses are treated as one number; thus
We read ( a + b ) either as a plus b or as the quantity a plus b, if just saying a plus b might lead to confusion. Thus, if we said c times a plus b we might mean ca + b , though we would read ca + b as ca plus b . If we say c times the quantity a plus b , it is clear that we mean c ( a + b ).
The idea of a probability is used frequently in this book. We might say, for instance, that in a string of symbols the probability of the j th symbol is p ( j ). We read this p of j .
The symbols might be words, numbers, or letters. We can imagine that the symbols are tabulated; various values of j can be taken as various numbers which refer to the symbols. , shows one way in which the numbers j can be assigned to the letters of the alphabet.
When we wish to refer to the probability of a particular letter, N for instance, we could, I suppose, refer to this as p (5), since 5 refers to N in the above table. Wed ordinarily simply write p (N), however.
What is this probability? It is the fraction of the number of letters in a long passage which are the letter in question. Thus, out of a million letters, close to 130,000 will be Es, so
| Value of j | Corresponding Letter |
|---|
| 1 | E |
| 2 | T |
| 3 | A |
| 4 | O |
| 5 | N |
| 6 | R |
| etc. |
Sometimes we speak of probabilities of two things occurring together, either in sequence or simultaneously. For instance, x may stand for the letter we send and y for the letter we receive. p ( x, y ) is the probability of sending x and receiving y. We read this p of x, y (we represent the comma by a pause). For instance, we might send the particular letter W and receive the particular letter B. The probability of this particular event would be written p (W, B). Other particular examples of p ( x, y ) are p (A, A), p (Q, S), p (E, E), etc. p ( x, y ) stands for all such instances.
We also have conditional probabilities. For instance, if I transmit x, what is the probability of receiving y ? We write this conditional probability p x ( y ). We read this p sub x of y . Many authors write such a conditional probability p ( y | x ), which can be read as, the probability of y given x . I have used the same notation which Shannon used in his original paper on communication theory.
Let us now write down a simple mathematical relation and interpret it:
p ( x, y ) = p ( x ) p x ( y )
That is, the probability of encountering x and y together is the probability of encountering x times the probability of encountering y , when we do encounter x . Or it may seem clearer to say that the number of times we find x and y together must be the number of times we find x times the fraction of times that y , rather than some other letter, is associated with x .
We frequently want to add many things up; we represent this by means of the summation sign , which is the Greek letter sigma. Suppose that j stands for an integer, so that j may be 0, 1, 2, 3, 4, 5, etc. Suppose we want to represent
0+1+2+3+4+5+6+7+8 8
which of course is equal to 36. We write this
We read this, the sum of j from j equals 0 to j equals 8. The sign means sum. The j = 0 at the bottom means to start with 0, and the j = 8 at the top means to stop with 8. The j to the right of the sign means that what we are summing is just the integers themselves.