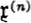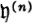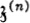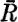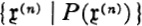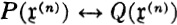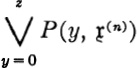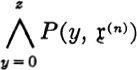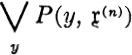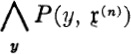Martin Davis - Computability and Unsolvability

Computability & Unsolvability

MARTIN DAVIS Department of Mathematics and Computer Sciences
Courant Institute of Mathematical Sciences
New York University DOVER PUBLICATIONS, INC.
NEW YORK Copyright 1958, 1973, 1982 by Martin Davis. Copyright 1973 by The Mathematical Association of America. All rights reserved under Pan American and International Copyright Conventions. This Dover edition, first published in 1982, is an enlarged version of the work originally published by McGraw-Hill Book Company, New York, in 1958. The Dover edition includes a new preface and a new appendix to the text. 80, No. 3, March 1973, pp. 233-269) and is reprinted here with the permission of The Mathematical Association of America, 1529 Eighteenth Street, N.W., Washington, D.C. 20036. 20036.

Manufactured in the United States of America
Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y. 11501 Library of Congress Cataloging in Publication Data Davis, Martin, 1928 Computability & unsolvability. Reprint. Originally published : New York : McGraw-Hill, 1958. (McGraw-Hill series in information processing and computers) Includes bibliographical references and index. 1.

Recursive functions. 2. Unsolvability (Mathematical logic) 3. Computable functions. I. II. II.

Series: McGraw-Hill series in information processing and computers.

QA9.6.5.D38 1982	511.3	82-7287
ISBN 0-486-61471-9 (pbk.)	AACR2

To Virginia Work in computer science over the past two decades has amply justified the hope expressed in the original preface to this book that the general theory of computability, and in particular Turings model of computation, would play an important role in the theory of digital computers. In fact, much of the terminology introduced here has become a standard part of the terminology of theoretical computer science, and many computer scientists have told me that this book was their theoretical introduction. Naturally I am delighted that my first book continues to find an audience, and that it will live on in this Dover edition. One of the great pleasures of my life came in February 1970, when I learned of the work of Yuri Matiyasevi which completed the proof of the crucial conjecture in . MARTIN DAVIS 1982 This book is an introduction to the theory of computability and non-computability, usually referred to as the theory of recursive functions.

This subject is concerned with the existence of purely mechanical procedures for solving various problems. Although the theory is a branch of pure mathematics, it is, because of its relevance to certain philosophical questions and to the theory of digital computers, of potential interest to nonmathematicians. The existence of absolutely unsolvable problems and the Gdel incompleteness theorem are among the results in the theory of computability which have philosophical significance. The existence of universal Turing machines, another result of the theory, confirms the belief of those working with digital computers that it is possible to construct a single all-purpose digital computer on which can be programmed (subject of course to limitations of time and memory capacity) any problem that could be programmed for any conceivable deterministic digital computer. This assertion is sometimes heard in the strengthened form: anything that can be made completely precise can be programmed for an all-purpose digital computer. However, in this form, the assertion is false.

In fact, one of the basic results of the theory of computability (namely, the existence of nonrecursive, recursively enumerable sets) may be interpreted as asserting the possibility of programming a given computer in such a way that it is impossible to program a computer (either a copy of the given computer or another machine) so as to determine whether or not a given item will be part of the output of the given computer. Another result (the unsolvability of the halting problem) may be interpreted as implying the impossibility of constructing a program for determining whether or not an arbitrary given program is free of loops. Because it was my aim to make the theory of computability accessible to persons of diverse backgrounds and interests, I have been careful (particularly in the first seven chapters) to assume no special mathematical training on the readers part. For this reason also, I was very pleased when the McGraw-Hill Book Company suggested that the book be included in its Information Processing and Computers Series. Although there is little in this volume that is actually new, the expert will perhaps find some novelty in the arrangement and treatment of certain topics. In particular, the notion of Turing machine has been made central in the development.

This seemed desirable, on the one hand, because of the intuitive suggestiveness of Turing machines and the analogies between them and actual digital computers and, on the other hand, because combining Turings approach with the powerful syntactic methods of Gdel and Kleene makes it possible to present the various aspects of the theory of computability, from Posts normal systems to the Kleene hierarchy, in a unified manner. Some of the material in this book was used in a graduate course, given by me, at the University of Illinois and in lecture series at the Control Systems Laboratory of the University of Illinois and at the Bell Telephone Laboratories. Part of the work for this book was done while the author was at the Institute for Advanced Study on a grant from the Office of Naval Research. The book could be used as a text, or supplementary text, in courses in mathematical logic or in the theory of computability. I should like to thank Mr. Donald Kreider, Professor Hilary Putnam, Professor Hartley Rogers, Jr., and Dr.

Norman Shapiro for suggesting many corrections and improvements. MARTIN DAVIS

References in this glossary are to the page(s) where the symbol in question is introduced.

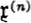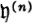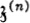mS

mS

RS

RS

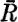RS

CC(x1,...., xx)

pq

pq

p

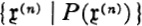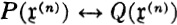CP(x1,... , xn)

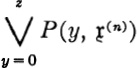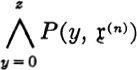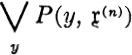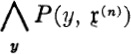Next page