Math is weird. Numbers go on foreverand there are different kinds of forever. Prime numbers help cicadas survive. A (mathematical) ball can be cut up and then put back together, without any gaps, to make a ball twice the size, or a million times the size, of the original. There are shapes that have fractional dimensions and curves that fill a plane, leaving no holes. While bored by a dull presentation, physicist Stanislaw Ulam wrote out numbers, starting from 0, in a spiral form, marked in all the prime numbers, and found that many primes lie on long diagonalsa fact that is still not fully unexplained.
We forget sometimes how weird math is because were so used to dealing with what seem like ordinary numbers and calculations, the stuff we learn about in school or use every day. Yet the fact that our brains are so adept at thinking mathematically, and, if we choose, to doing really complex and abstract math, is surprising. After all, our ancestors, tens or hundreds of thousands of years ago, didnt need to solve differential equations or dabble in abstract algebra in order to stay alive long enough to pass on their genes to the next generation. While they searched for their next meal or a place to shelter, there was nothing to be gained from musing about geometry in higher dimensions or theories of prime numbers. Yet were born with brains that have the potential to do these things and to uncover, with each passing year, more and more extraordinary truths about the mathematical universe. Evolution has provided us with this skill, but how and why? Why are we, as a species, so good at doing something that has every appearance of being just an intellectual game?
Somehow math is woven into the very fabric of reality. Dig deep enough, and we find that what seemed to be tangible bits of matter or energyelectrons or photons, for instancedissolve into immateriality, becoming mere waves of probability, and all were left with is a ghostly calling card in the form of some intricate but beautiful set of equations. In some sense, mathematics underpins the physical world around us, forming an invisible infrastructure. Yet it also goes beyond this, into abstract realms of possibility that may forever remain purely exercises of the mind.
Weve chosen in this book to highlight some of the more extraordinary and fascinating areas of math, including those where exciting new developments are in the offing. In some cases, they have links with science and technologyparticle physics, cosmology, quantum computers, and the like. In others, they represent, for now at least, math for maths sake and are adventures into an unfamiliar land that exists only in the minds eye. Weve chosen not to shy away from certain subjects just because theyre hard. One of the challenges in describing many aspects of math for a general audience is that theyre far removed from everyday experience. But in the end, some way can always be found to link what todays explorers and pioneers at the frontiers of mathematics are doing with the world of the familiar, even if the language we have to use isnt as precise as academics would ideally choose. Its perhaps true to say that if something, however obscure, cant be explained reasonably well to a person of normal intelligence, then the explainer needs to improve their understanding!
This book came about in an unusual way. One of us (David) has been a science writer for more than thirty-five years and has written many books on astronomy, cosmology, physics, and philosophy, even an encyclopedia of recreational math. The other (Agnijo) is a brilliant young mathematician and child genius, with an IQ of at least 162, according to Mensa, who, at the time of writing, has just finished training in Hungary in preparation for the 2017 International Mathematics Olympiad. Agnijo started coming to David for tuition in math and science at the age of twelve. Three years later, we decided to write a book together.
We sat down and brainstormed the topics we wanted to cover. David, for instance, came up with higher dimensions, the philosophy of math, and the math of music, while Agnijo was keen to write about large numbers (his personal passion), computation, and the mysteries of primes. Right from the start, we chose to lean toward anything unusual or downright weird and to connect this weird math, where possible, with real-world issues and everyday experience. We also made a commitment not to shy away from subjects just because they were tough, adopting as a mantra that if we cant explain something in plain language, then we dont properly understand it. David generally took on the historical, philosophical, and anecdotal aspects of each chapter, while Agnijo grappled with the more technical aspects. Agnijo fact-checked Davids work, and David combined all the writing into finished chapters. It all worked surprisingly well! We hope you enjoy the result.
In glancing through the pages of this book, you may notice that it contains some symbols, including xs, s (omegas), and even the odd 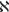 (aleph). Youll find an occasional equation or an unfamiliar-looking combination of characters, such as 333 (especially in the chapters on large numbers and infinity). If youre a nonmathematician, dont be put off. Theyre just shorthand for ideas that, hopefully, we explain well enough in advance and thereby help us delve a little faster and deeper into the subject than would otherwise be possible. One of us (David) has taught math privately to students for many years and has yet to come across one who cant be good at it once they believe in themselves. The fact is that were all natural mathematicians, whether we realize it or not. So, with that in mind, lets take the plunge.
(aleph). Youll find an occasional equation or an unfamiliar-looking combination of characters, such as 333 (especially in the chapters on large numbers and infinity). If youre a nonmathematician, dont be put off. Theyre just shorthand for ideas that, hopefully, we explain well enough in advance and thereby help us delve a little faster and deeper into the subject than would otherwise be possible. One of us (David) has taught math privately to students for many years and has yet to come across one who cant be good at it once they believe in themselves. The fact is that were all natural mathematicians, whether we realize it or not. So, with that in mind, lets take the plunge.














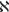 (aleph). Youll find an occasional equation or an unfamiliar-looking combination of characters, such as 333 (especially in the chapters on large numbers and infinity). If youre a nonmathematician, dont be put off. Theyre just shorthand for ideas that, hopefully, we explain well enough in advance and thereby help us delve a little faster and deeper into the subject than would otherwise be possible. One of us (David) has taught math privately to students for many years and has yet to come across one who cant be good at it once they believe in themselves. The fact is that were all natural mathematicians, whether we realize it or not. So, with that in mind, lets take the plunge.
(aleph). Youll find an occasional equation or an unfamiliar-looking combination of characters, such as 333 (especially in the chapters on large numbers and infinity). If youre a nonmathematician, dont be put off. Theyre just shorthand for ideas that, hopefully, we explain well enough in advance and thereby help us delve a little faster and deeper into the subject than would otherwise be possible. One of us (David) has taught math privately to students for many years and has yet to come across one who cant be good at it once they believe in themselves. The fact is that were all natural mathematicians, whether we realize it or not. So, with that in mind, lets take the plunge.