Andrew Witt - Formulations: Architecture, Mathematics, Culture

1. Chapter 1
2. Chapter 2
3. Chapter 3
4. Chapter 4
5. Chapter 5
6. Chapter 6
7. Chapter 7
8. Chapter 8
9. Chapter 9
10. Chapter 10

for Athena

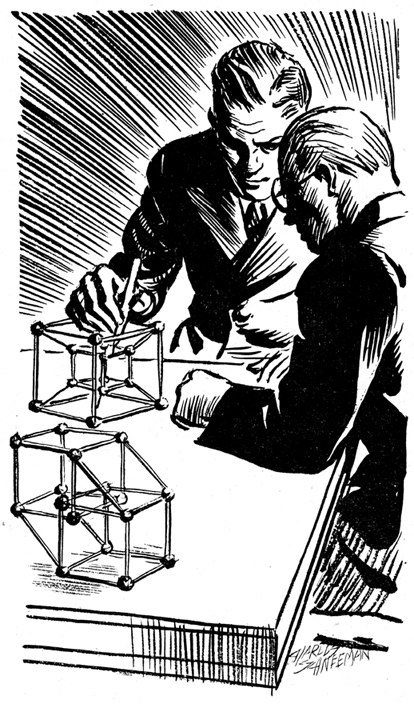
1.1 The architect Quintus Teal examines models of his hypercubic house. Robert Heinlein, And He Built a Crooked House, Astounding Science Fiction (February 1941): 69.

Source: Schneeman (Charles e .) Papers, d -238, Special Collections, uc Davis Library.

Courtesy of the family of the artist.

fig. 1.1

In Robert Heinlein's 1941 short story And He Built a Crooked House, the iconoclastic young designer Quintus Teal proposes an architecture elaborated from the logic of four-dimensional crystals. Seeing the remarkable design freedoms and spatial economies of advanced mathematics, he aspires to move beyond the geometric limitations of his contemporaries toward a new architecture:

Mined from advanced mathematics, the complexities and contradictions of this architecture multiply, leading to the story's surreal conclusion (to which we shall return). Fantastic as it may seem, this fiction was paralleled to a remarkable degree by ever-deeper architectural fascination with modern mathematics in mid-twentieth-century design culture. In fact, exactly the methods that Quintus Teal mentionssuch as modular structures and homomorphologywere taken up by architects who saw in advanced mathematics a portal to dizzying new spaces and practices, unerringly precise and resolutely contemporary.

Inspired partly by the beguiling mathematical maquettes and scientific models of eccentric geometric objects, Bill eschewed more classical associations of geometric proportion to exult in abstract and modern varieties of mathematics. He saw fields like differential and topological geometry as templates for new design tactics. His hoped-for synthesis of technical precision and visual creation was symptomatic of a new subculture of design that absorbed mathematical ideas and representations, modeling the entire project of visual research on quantitative methods and on the pattern of scientific epistemologies.

Equally relevant from an architectural perspective are the signifying practices of mathematical drawing and diagramming, visual tactics resonant with their architectural analogues. Mathematical formulations furnish designers a means to exceed subjectivity through universal and inviolate facts of form, and a medium to estrange the intuition to the point of fresh creation. The historical lineages of mathematized design and its signifying practices offer periodic tables and catalogs of formulationsepistemic, logical, formal, socialthat function as lexicons of mathematical writing and sourcebooks of mathematical drawing for precise practices of creation.

History offers an abundance of hackneyed odes to the mystic transcendence of number in architecture:

Enthusiastic as they may be, these sentiments of Le Corbusier are characteristic of a rhetorical obscurantism around mathematics in modern design that rests on a brittle bric-a-brac foundation of natural forms and mystic associationsthe golden ratio, the nautilus shell, tedious references to musical rhythm, or the endless parade of anthropometric proportions. Both historians and popularizers have too often reduced geometry in architecture to mere symmetry or pattern. Such lazy associations have debased conversations on mathematics in architecture to a hopelessly caricatured level.

Yet his substitution of the narrower category of geometric proportion for the wider field of mathematics can leave the impression of false equivalence. The more nuanced argument is lost and instead a caricature of Rowe persists as an alibi for a technically impoverished notion of mathematics in architecture.

Prior considerations of mathematics and architecture have often neglected the surprising and sometimes rigorous architectural encounters with a breadth of calculational systems over the course of the last century, including in the more abstract varieties of mathematics such as matrix analysis, polyhedral geometry, and information theory. Architects like Anne Tyng, Steve Baer, William Huff, Peter Pearce, and Lionel March took these methods seriously, inventively retooling them for design. They deployed a staggering range of mathematical techniques, from the elementary to the fantastically arcane, each adopted with various degrees of reverence and opportunism. For these and other architects, mathematics in design took on instrumental and teleological undertones, being both a set of techniques and a point of view freighted with ideological associations. Mathematical design is a dauntingly vast territory, practically a discipline in its own right, highly variegated, political, and contested.

For certain architects, mathematics was a conceptual intermediary for the rapprochement of natural sciences with creative method. In fact, mathematics has often been a lens through which sciences such as biology and chemistry were understood and ultimately operationalized by architects. The role of mathematics vis--vis architecture essentially situates design's entire position relative to the natural sciences.

For Evans, accepted practices of drawing circumscribed the experimental horizons of architecture, ensuring that design encountered mathematics only in the narrow cul-de-sac of constructed geometry. For the architect, modern mathematics was an enticing but inaccessible mirage.

By registering a much wider spectrum of conceptual and methodological interactions between design culture and mathematical thought, I argue that architects went well beyond the mere allusions to advanced mathematics to which Evans claimed they were confined. While metaphorical invocations of mathematics were indeed among the earliest type, by 1970 certain architects had gradually assimilated quantitative means to address a range of unseen hyperdimensional forces. In the case studies that follow, architects are not merely alluding to advanced mathematical techniques but using them and training other designers to do the same. Moreover, Evans's limited identification of nineteenth-century mathematics with hyperdimensionality neglects epochal methods of drawing and modeling from other nascent branches of mathematics like geodesy, topology, crystallography, graph theory, and others that were appropriated by architects as engines to represent both designed buildings and more abstract spatial relationships. In fact, by the mid-twentieth century, calculational methods of transcription and encoding with roots in nineteenth and turn-of-the-century mathematics began to provide compelling alternatives to the accepted representational and methodological canons of architecture. A mathematical turn was well under way.

Yet, for a discipline that places considerable weight on an almost familial continuity of apprenticeship, reconstructing this mathematical turn presents many challenges. With no recognized lineage of mathematical experimentalism and no continuous institutional project of design mathematics, the transmission of mathematical knowledge has been halting, sporadic, and incomplete. The inescapable gaps, fissures, and discontinuities that mark the terrain demand a forensic piecing together of a mosaic of vignettes, fragment by fragment, to hint at a more complete map.