A.W.F. Edwards - Pascals Arithmetical Triangle: The Story of a Mathematical Idea

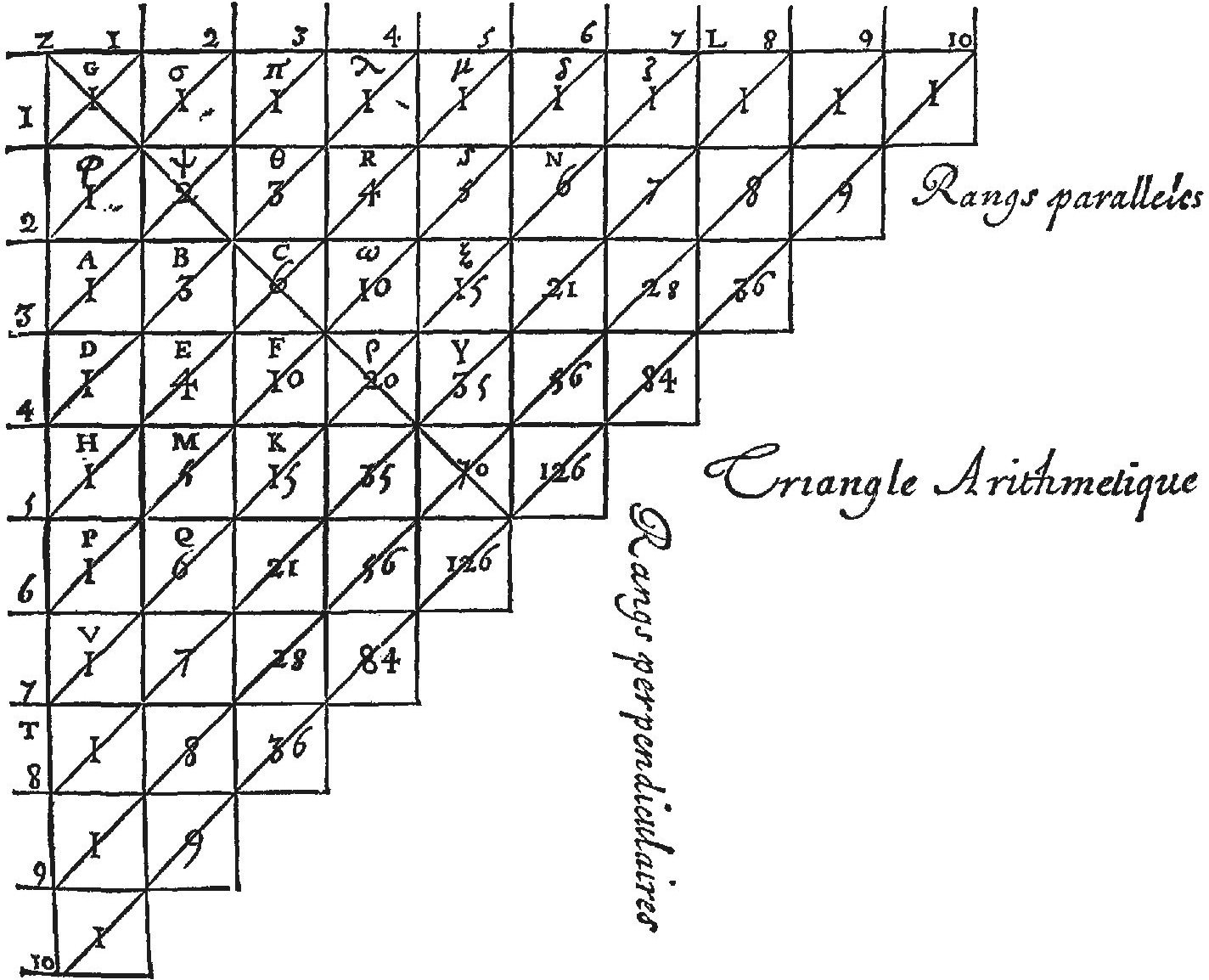
Pascal's original Arithmetical Triangle, from the Trait du triangle arithmtique (1665)

Copyright

Copyright 1987, 2002, 2019 by A. W. F. Edwards

All rights reserved.

Bibliographical Note

This Dover edition, first published in 2019, is an unabridged and slightly corrected republication of the work originally printed by Johns Hopkins University Press, Baltimore, Maryland, in 2002. [First publication: Oxford University Press, 1987.] A new frontispiece has been included in this volume.

Library of Congress Cataloging-in-Publication Data

Names: Edwards, A. W. F. (Anthony William Fairbank), 1935 author.

Title: Pascal's arithmetical triangle: the story of a mathematical idea / A. W. F. Edwards, ScD, FRS (emeritus professor of biometry, University of Cambridge; Fellow of Gonville and Caius College).

Description: 2019 Dover edition. | Mineola, New York: Dover Publications, Inc., 2019. | Originally published: London: C. Griffin ; New York: Oxford University Press, 1987. Reissued: Baltimore, Maryland: Johns Hopkins University Press, 2002. A republication of the 2002 version by Johns Hopkins University Press. | Includes bibliographical references and index.

Identifiers: LCCN 2018052526 | ISBN 9780486832791 | ISBN 0486832791

Subjects: LCSH: Pascal's triangle. | Binomial coefficients.

Classification: LCC QA241 .E37 2019 | DDC 512/.7dc23

LC record available at https://lccn.loc.gov/2018052526

Manufactured in the United States by LSC Communications

83279101 2019

www.doverpublications.com

For CATHARINA

PASCAL'S ARITHMETICAL TRIANGLE

Inexhaustae Scientiae TABVLA secretissima Arithmetices Arcana pandens.

FAULHABER (attrib.), 1615

[A rich mine of information in the form of a TABLE which unfolds the most recondite secrets of arithmetic]

Plena haec mysteriis pulcherrimis tabella.

OUGHTRED, 1631

[This table full of the most beautiful mysteries.]

Abacus .

BRIGGS, 1633

[A calculator useful for everything.]

C'est une chose trange combien il est fertile en proprits.

PASCAL, 1654

Habet haec Tabula proprietates plane eximias & admirandas; praeterquam enim quod Combinationum mysterium in illa latere jam ostendimus, notum est interioris Geometriae peritis, praecipua etiam totius reliquae Matheseos arcana inibi delitescere.

JAMES BERNOULLI, 1713

[This Table has truly exceptional and admirable properties; for besides concealing within itself the mysteries of Combinations, as we have seen, it is known by those expert in the higher parts of Mathematics also to hold the foremost secrets of the whole of the rest of the subject.]

The contemplation of this table has probably been attended with the invention and extension of some of our most curious discoveries in mathematics, both in regard to the powers of a binomial, with the consequent extraction of roots, the doctrine of angular sections by Vieta, and the differential method by Briggs and others.

HUTTON, 1786

Contents

NOTE

All works cited thus: Pascal (1665), in the notes at the end of each chapter, are listed in the References on . The date used is that of the original publication of the work cited, though the page reference may be to a more recent edition. Works written before the invention of printing are given the date of writing, which will often be only approximate. There are no references listed with dates Before Christ, so that all dates are to be interpreted A.D. In the case of references to material that was not published for many years after it was written, such as Fermat's correspondence, the date of writing is used.

The intention is thus to combine a reference system with an approximate chronology, though the great variety of source material has inevitably led to many compromises.

Preface to the Johns Hopkins edition

The origins of this book lie in my undergraduate training in genetics in 1956, and since they involve one of the greatest scientists of the twentieth century, R. A. Fisher, about whom any anecdote is worth recording, I shall risk a charge of self-indulgence and describe several.

In 1956 Fisher, aged 66, was in his last year as the Professor of Genetics at Cambridge, and I was the sole student accepted to read genetics in this, my last (third) undergraduate year. I knew very little statistics, so at the end of one of Fisher's early lectures I asked him how I should learn some. With a twinkle in his eye he remarked that he had written one or two books on statistics, and perhaps I might start by reading them. I bought Statistical Methods for Research Workers (12th ed.) and The Design of Experiments (6th ed.) and began with the former. I encountered the binomial distribution in Chapter III, "Distributions," and was fascinated by Fisher's description of fitting it to some extensive data on the distribution of the sexes in families of eight children. He points out the excess variance in the data, and, after rejecting as a possible explanation the inclusion of multiple births, especially twins, he leaves the reader to think of his own explanation.

It occurred to me that a binomial distribution in which the sole parameter (in this case the probability of a male birth) varied from sample to sample would display this excess variance. By a stroke of good fortune, I had just learned from some lectures I had recently attended that a distribution called the "" was appropriate for describing such variation. I applied it to the parameter of the binomial distribution, performed the necessary integration, and was delighted to find that it "came out." Of course, I later learned that the resulting "-binomial distribution" was not new, but the thrill of discovery cast a warm glow over everything to do with binomial coefficients. There was a calculator (electro-mechanical) in the departmental library and I used it to fit the new distribution to the data; when Fisher came in and saw what I was doing he reprimanded me for not concentrating on my forthcoming examinations, but his tone belied his words, for he was glad to see a student taking an initiative. Later, as a graduate student, I gave my first seminaron the "Binomial Distribution." Fisher sat quietly through it, and I do not recall any comments.

As the years went by I collected many results involving binomial coefficients, and during my Christmas vacation of 1978 I settled down to write a little book about them; the first half to treat their purely mathematical properties, and the second some of their applications. When nearly complete I decided to add a brief account of their history, only to find that the books I had consulted in the history of mathematics were often in error. Early on in my attempt to rectify this I called for one of the two copies of Pascal's Trait du triangle arithmtique from Cambridge University Library and discovered to my astonishment that Pascal had, already in 1654, written the book I had just finished in exactly the format I had chosenpure mathematics first, applications second.

It is not often that an author finds himself forestalled by 324 years. My reaction was to write Pascal's Arithmetical Triangle to help remedy the ignorance surrounding the history of the Arithmetical Triangle and Pascal's role in it. The book was practically complete by 1981 but, after several rejections, was not published until 1987. Even then it was hardly noticed because the publisher forgot to send out any review copies, and when they were finally dispatched the journals said the book was too old to review. Nevertheless, perhaps