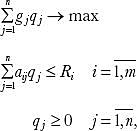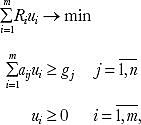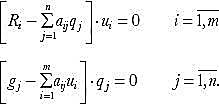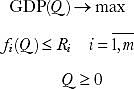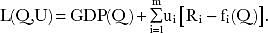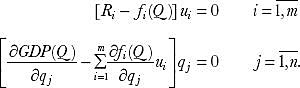Ashot Tavadyan - Uncertainty Bands: A Guide to Predicting and Regulating Economic Processes

The precise definition of economic indicators is impossible in any model, even if the model represents the economy in an extremely simplified form. It is only possible to formulate their ratio in general terms.

Illustrative examples of models are used herein since the complexity of the model is not critical for describing generalized functional interdependencies between indicators.

Below is an example of a simplified quantitative economic model:

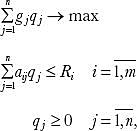
where gj is the share of income in the price of the product j, ij is the expenses of the i-th resource in the unit production of the j-th product, Ri is the volume of the i-th resource and qj is the volume of product j.

The dual problem of the considered model is formulated below:

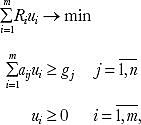
where ui is the optimal valuation of the i-th resource.

From the duality principle the optimal values satisfy the following conditions:

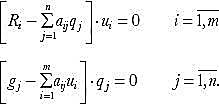
In the primal problem, the volumes of resources Ri, the share of income gj, the objective function of the direct problem and technological rates of resource consumption are known. Resources ui and volume of output qj are unknown and to be determined. It can be observed from the obtained ratio that if ui and qj are known, then the values of Ri and gj can be determined. Therefore, for any given set of variables, the optimal values of others can be obtained.

Thus, if a model contains price variables gj and ui while it is necessary to determine quantitative variables qj and Ri, then separately for both quantitative and price variables m + n linear equations with m + n unknowns can be obtained. Provided that the coefficients of the unknowns are positive, the rank of the matrix composed of the coefficients of the unknowns will be equal to m + n; in so doing, the quantitative variables will be found. Under the same condition, if quantitative variables are given, then price variables will be found.

Likewise, in any optimization model, point estimates of one group of quantitative and price variables can be found if only the other group is assigned a value. To determine some variables, the values of other variables must be taken for granted in advance.

The relations of presented quantitative and price indicators do not infer that the change in the volume of output is necessarily the cause of change in price indicators since their causality is not always unambiguous.

Similar ratios can be obtained when choosing the main target indicator for GDP growth, exports or employment. Similar ratios can be obtained for nonlinear models.

Below is a generalized optimization model of economic growth:

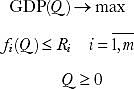
The model requires resource constraints to be met.

The Lagrange function for the general optimization model for economic growth is as follows:

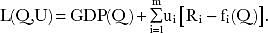
The relations below follow the KuhnTucker conditions for optimal economic indicators:

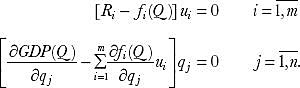
Given that m + n quantitative variables of GDP and resource constraints are known, it would seem possible to determine their price variables and vice versa. However, in optimization models that characterize generalized causal links of economy, quantitative variables only formally define price variables. The converse holds as well. Moreover, this is true for any combination of variables.

1. A. A. Tavadyan, Uncertainty Intervals of Economics (Moscow: Nauka, 2012).

A real process may not be subject to measuring, nor be exactly measured, for the economic situation is continually subject to critical alteration, with periodical considerable perturbations.

It is to be recognized that there are no methods for precise measuring of the economic processes. Thus, when quantitatively formulating the precisely indeterminate processes, it must be identified whether its evaluation is distorted. The interval-based method is particularly useful for processes that cannot be precisely measured or predicted due to subjective or even objective reasons, for it will enable to describe the process while discovering its essence with no distortions.

A point estimate of an economic indicator often results in the loss of several of its attributes; hence, the book presents the interval method enabling quantifying the process with minimal losses in determining the indicator attributes. It is the indicative estimation of the process attributes manifested in the reality that will give a systemic picture of the quantitative and qualitative features of said process.

The interval method will enable a most complete description to be made of the essence and the manifestation of the real processes; hence, fully satisfying is the principle of Occams razor which can be regarded as a sufficient condition for the application of this method. Given the impossibility of accurate measurement in the economy, the interval method allows us to overcome the complexity of describing economic processes.

The interval determination of indicators is a method of research for precisely indeterminate indicators under the state of uncertainty natural for the economy. The interval representation of the indicator will enable a description to be made of its most likely values. The interval method of economic indicators will open a logical path from the predicament of explaining its quantitatively precise indefinability. It will help to deploy a complete picture of causal links in the economy.

The capabilities of the existing methods of evaluation and forecasting the economic indicators cannot be seen as an absolute cure-all. This is no less hazardous than their complete disregard. Meanwhile, for an efficient quantitative analysis of economic processes, it is necessary to determine the content of economic causal links and the dependencies of the indicators. Only after that is done the quantitative analysis will become coherent to the essence of reality and yield meaningful results.

Quantitative changes may occur even if the essential attributes of reality are identical. This once again emphasizes the expedient nature of the interval method. The method also specifies the quantitative features based on the essential attributes underlying any study. This makes the interval method an efficient tool when analyzing the economy.

The interval method of analyzing the economic processes enables both the optimal combination of qualitative and quantitative methods of exploring the economic indicators and their systematization.