Michael J. Campbell - Statistics at Square Two

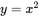It is simple to understand raising a quantity to a power, so that: is equivalent to: 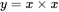. This can be generalised to: 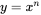for arbitrary n so 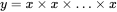n times.

A simple result is that:

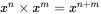(A1.1)

for arbitrary n and m. Thus, for example 32 34 = 36 = 729. It can be shown that this holds for any values of m and n, not just whole numbers.

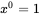We define: , because: .

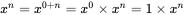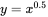A useful extension of the concept of powers is to let n take fractional or negative values. Thus: can be shown to be equivalent to: 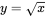, because: 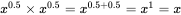and also: .

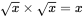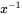Also: can be shown equivalent to 1/x, because: .

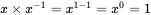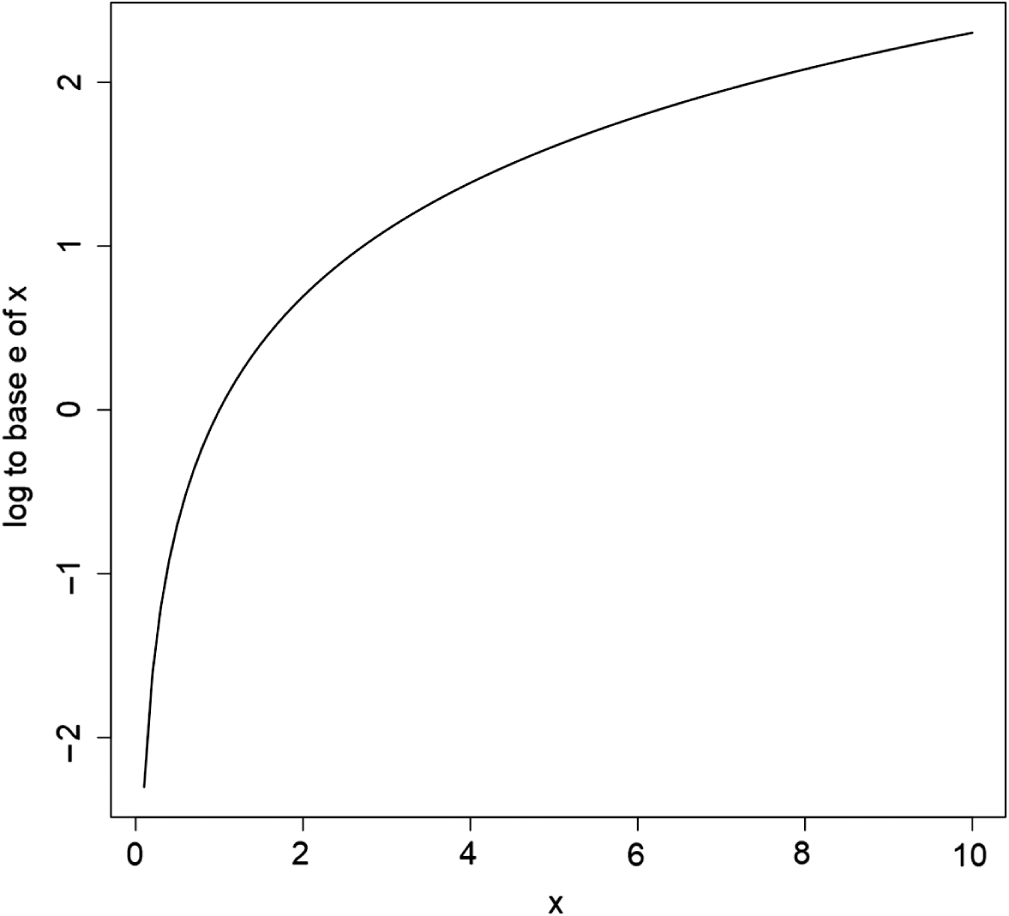
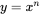If , then the definition of a logarithm of y to the base x is the power that x has to be raised to get y. This is written: 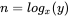or n equals log to the base x of y.

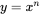Suppose and 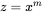. It can be shown from Equation A1.1 that: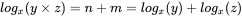

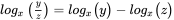
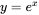Thus, when we multiply two numbers we add their logs. This was the basis of the original use of logarithms in that they enabled a transformation whereby arithmetic using multiplications could be done using additions, which are much easier to do by hand. In Appendix 2 we need an equivalent result, namely that:

In other words, when we log transform the ratio of two numbers we subtract the logs of the two numbers.

The two most common bases are 10, and a strange quantity: e = 2.718, where the dots indicate that the decimals go on indefinitely. This number e has the useful property that the slope of the curve: at any point (x, y) is just y, whereas for all other bases the slope is proportional to y but not exactly equal to it. The formula: 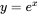is often written: 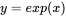. The logarithms to base e and 10 are often denoted ln and log respectively on calculators, and log and log10 in R. Logs to base e are often called the natural logarithm. In this book all logarithms are natural, that is to base e. We can get from one base to the other by noting that: 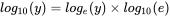. To find the value of e in R use the fact that: 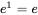, thus:

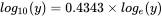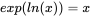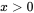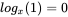Thus: .

Note, log is just the inverse function to exponential so: .

For example if x = 23:

Note, it follows from the definition that for any: , .

In this book exponentials and logarithms feature in a number of places. It is much easier to model data as additive terms in a linear predictor and yet often terms, such as risk, behave multiplicatively, as discussed in . The line does not plateau, but the rate of increase gets smaller as x increases.

Loge(x) vs x.

This appendix gives a brief introduction to the use of maximum likelihood, which was the method used to fit the models in the earlier chapters. We describe the Wald test and the likelihood ratio (LR) test and link the latter to the deviance. Further details are given in Clayton and Hills.

A model is a structure for describing data and consists of two parts. The first part describes how the explanatory variables are combined in a linear fashion to give a linear predictor. This is then transformed by a function known as a link function to give predicted or fitted values of the outcome variable for an individual. The second part of the model describes the probability distribution of the outcome variable about the predicted value.

Perhaps the simplest model is the Binomial model. An event happens with a probability . Suppose the event is the probability of giving birth to a boy and suppose we had five expectant mothers who subsequently gave birth to two boys and three girls. The boys were born to mothers numbered 1 and 3. If is the probability of a boy the probability of this sequence of events occurring is (1 ) (1 ) (1 ). If the mothers had different characteristics, say their age, we might wish to distinguish them and write the probability of a boy for mother