LEVELS OF
INFINITY
SELECTED WRITINGS ON
MATHEMATICS AND PHILOSOPHY
HERMANN WEYL
TRANSLATED AND EDITED WITH AN
INTRODUCTION AND NOTES BY
PETER PESIC
St. Johns College
Santa Fe, New Mexico
DOVER PUBLICATIONS, INC.
Mineola, New York
Copyright
Copyright 2012 by Peter Pesic
All rights reserved.
Bibliographical Note
A compilation of essays by Hermann Weyl, Levels of Infinity is a new work, first published by Dover Publications, Inc., in 2012.
International Standard Book Number
ISBN-13: 978-0-486-26693-0
Manufactured in the United States by Courier Corporation
48903501
www.doverpublications.com
Introduction
A Proteus who transforms himself ceaselessly in order to elude the grip of his adversary, not becoming himself again until after the final victory. Thus Hermann Weyl (18851955) appeared to his eminent younger colleagues Claude Chevalley and Andr Weil. Surprising words to describe a mathematician, but apt for the amazing variety of shapes and forms in which Weyls extraordinary abilities revealed themselves, for among all the mathematicians who began their working life in the twentieth century, Herman Weyl was the one who made major contributions in the greatest number of different fields. He alone could stand comparison with the last great universal mathematicians of the nineteenth century, Hilbert and Poincar, in the view of Freeman Dyson. He was indeed not only a great mathematician but a great mathematical writer, wrote another colleague. This anthology presents a spectrum of Weyls later mathematical writings, which together give a portrait of the man and the mathematician. The works included have been chosen for their accessibility, but they do also include, where needed, the mathematical details that give vivid specificity to his account. Weyls essays will convey pleasure and profit both to general readers, curious to learn directly from a master mathematician, as well as to those more versed, who want to study his unique vision. Those who wish to explore further his seminal work in physics in its philosophic and mathematical contexts will find relevant writings in a companion anthology, Mind and Nature [2009a], which gathers his writings in these fields; as a result of Weyls inclusive vision, these two anthologies overlap and complement each other at many points.
The protean Weyl drew his many shapes from rich and complex life-experience, in which mathematics formed only one strand in a complex tapestry. Already philosophic in temperament as a teenager who pored over Kant, Weyl was deeply formed by his work with David Hilbert, his teacher and mentor at the University of Gttingen. Weyl recalled being a country lad of eighteen who became entranced by Hilbert, a Pied Piper seducing so many rats to follow him into the deep river of mathematics.
There he met Albert Einstein, who during 19131914 was in the midst of Though the initial hopes for this theory faded in the light of difficulties noted by Einstein (and later the need to incorporate quantum theory), Weyl continued to ponder the generalizations and implications of his 1918 theory. Looking back, Weyls work laid the foundation of the gauge theories that, fifty years later, unified the strong, weak, and electromagnetic theories, fulfilling his initial aspiration in ways he had not dreamed.
Weyl eventually succeeded Hilbert at Gttingen, though only after protracted hesitation: first offered a professorship there in 1923 (to replace Felix Klein, another great mathematician important to his development), Weyl refused, happier to remain in Zrich, where he could find relief for his asthma in the mountains. He finally accepted the call to Gttingen in 1930, when Hilbert himself retired. The first essay in this volume dates from that year, as the newly-appointed Weyl travelled to Jena to speak to mathematics students. This essay, Levels of Infinity, was not included in Weyls collected papers and has not been reprinted since 1931 nor ever before translated into English. It gives an arresting portrait of his intellectual development and his struggle with basic questions in the foundations of mathematics.
Though devoted to Hilbert, Weyl for a time sided against him in an ongoing controversy that continues to simmer under the surface of mathematical practice. In the course of introducing unheard-of levels and degrees of infinity during the 1880s, Georg Cantor opened new mathematical realms that excited but also disturbed thoughtful practitioners.
To that end, Brouwer disallowed the use of the principle of the excluded middle that any proposition either is true or its negation is true especially when applied to infinite sets. This principle could be applied to argue that, if the negation of some mathematical proposition is demonstrably false, therefore the proposition must be true merely by elimination, without providing a positive demonstration. Brouwer advocated abandoning such propositions as not proven. For instance, let us examine the proposition there exist two irrational quantities a and b such that ab is rational. The Pythagoreans had already shown that 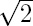 is irrational. Consider the quantity
is irrational. Consider the quantity 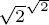 ; by the principle of the excluded middle, it is either rational or irrational. If it is rational, the proof is complete, for it exemplifies the quantity ab sought in the case
; by the principle of the excluded middle, it is either rational or irrational. If it is rational, the proof is complete, for it exemplifies the quantity ab sought in the case 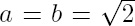 . If, on the contrary,
. If, on the contrary, 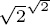 is irrational, then set
is irrational, then set 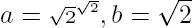 , so that
, so that
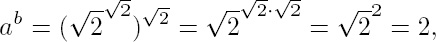
which is rational, thus implying that the proposition is true. From Brouwers point of view, though, the assumption that 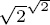 is rational must be supported by positive proof, not just used as a hypothesis in a proof by exclusion. Merely sidestepping the issue by moving the symbols around does not address the underlying question: what sort of existence does
is rational must be supported by positive proof, not just used as a hypothesis in a proof by exclusion. Merely sidestepping the issue by moving the symbols around does not address the underlying question: what sort of existence does 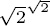 have?
have?
This critique had deep implications for the whole conduct of mathematics. For instance, Cantor had conjectured that no cardinal number lies between those denoting the countability of the integers, 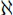 0, and the uncountable continuum of real numbers, c =
0, and the uncountable continuum of real numbers, c = 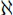 1. Brouwer considered this continuum hypothesis meaningless because the idea of numbering the continuum is an empty, abstract construct that lacks any intuitive substance, compared to our intuition of the integers. Most of set theory and large parts of analysis would have to be vacated, on Brouwers view. Ludwig Wittgenstein was also among those who considered that set theory was pernicious and wrong because it leads to utter nonsense in mathematics.
1. Brouwer considered this continuum hypothesis meaningless because the idea of numbering the continuum is an empty, abstract construct that lacks any intuitive substance, compared to our intuition of the integers. Most of set theory and large parts of analysis would have to be vacated, on Brouwers view. Ludwig Wittgenstein was also among those who considered that set theory was pernicious and wrong because it leads to utter nonsense in mathematics.












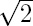 is irrational. Consider the quantity
is irrational. Consider the quantity 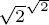 ; by the principle of the excluded middle, it is either rational or irrational. If it is rational, the proof is complete, for it exemplifies the quantity ab sought in the case
; by the principle of the excluded middle, it is either rational or irrational. If it is rational, the proof is complete, for it exemplifies the quantity ab sought in the case 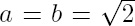 . If, on the contrary,
. If, on the contrary, 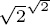 is irrational, then set
is irrational, then set 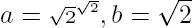 , so that
, so that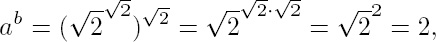
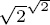 is rational must be supported by positive proof, not just used as a hypothesis in a proof by exclusion. Merely sidestepping the issue by moving the symbols around does not address the underlying question: what sort of existence does
is rational must be supported by positive proof, not just used as a hypothesis in a proof by exclusion. Merely sidestepping the issue by moving the symbols around does not address the underlying question: what sort of existence does 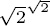 have?
have? 0, and the uncountable continuum of real numbers, c =
0, and the uncountable continuum of real numbers, c =