A CONCEPT
OF LIMITS
Donald W. Hight
Department of Mathematics
Pittsburg State University
Dover Publications, Inc., New York
To My Parents
My Appreciation of Them Is
tone Increasing and Unbounded Above
Copyright 1966, 1977 by Donald W. Hight.
All rights reserved.
This Dover edition, first published in 1977, is a corrected republication of the work first published by Prentice-Hall, Inc., Englewood Cliffs, N. J., in 1966. The section entitled Answers to Even-Numbered Exercises, published in 1966 by Prentice-Hall as a separate supplement, is here republished as an integral part of the book.
International Standard Book Number: eISBN 13: 978-0-486-15312-4
Library of Congress Catalog Card Number: 77-80029
Manufactured in the United States by Courier Corporation
63543006
www.doverpublications.com
P reface
LIMITS HAVE occupied a unique position in mathematics education. In secondary school or precalculus mathematics, they have been regarded as too hard and thus avoided; in calculus courses, they have been taken for granted or skimmed over hurriedly as if they were intuitively obvious. The purpose of this book is to extend a concept of limits from intuitive ideas about limits to knowledge of a generalized limit that is applicable in many areas of mathematics. To achieve this goal, a method has been employed that provides understanding through participation. Considerable effort has been made to allow and encourage each reader to progress at his own rate through a sequence of developmental steps from a known concept to a desired conclusion. Therefore, the book begins very slowly and assumes knowledge of high school algebra and an acquaintance with trigonometry. Then, it progresses through historical accounts of limits, the limits of sequences and functions, continuity, and proofs of theorems to the development and applications of a unifying concept of a generalized limit.
In addition to an understanding of a concept of limits, the book offers the following: motivated review and reinforcement of familiar topics such as algebra, inequalities, absolute value, functions, graphs, trigonometry, series, and geometry related to the measure of a circle; a thorough mathematical study of an important concept; the appreciation of definitions, proofs, and a mathematical structure; transition from typical precalculus and traditional mathematics to more sophisticated contemporary analysis; and some experience at limit-guessing and -finding.
is devoted to an intuitive and historical development of the limit of a sequence. The definition of a limit is preceded by Examples to Ponder, geometrical and historical examples, graphs, and repeated questions such as, For what values of n is sn within of L? Experience with the concept is provided by some simple theorems, proofs that some real number L is or is not the limit of a sequence 5, and helpful applications.
, functions are presented in greater detail in this section. Stress is placed upon simple theorems concerned with boundedness, uniqueness of limits, and positive or negative limits. Examples and exercises emphasize the interrelation of various types of limits, special limits, and continuity of trigonometric functions.
In , unifying attributes of the defined limits of sequences and functions are organized into a generalized limit. Then, by proving a single theorem for the generalized limit, a proof is given that is readily applicable to every type of limit previously discussed. The chapter also introduces limits and continuity of sums, differences, products, quotients, and composites of functions and concludes with applications of limits to high school mathematics, to calculus, and to extensions of the generalized limit theorems.
Mathematical terms that are especially associated with the presentation are written in boldface when they are introduced; similarly, important terms that have more widespread usage are written in italics.
Convention has been broken when it was thought that better understanding would result. Such expressions as 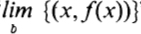 with
with 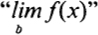 and lim {(n, sn)} with limsn are used to stress that a limit of a function or sequence has been defined and not a limit of a set of range values. Since students today may not think of a variable as a quantity that changes, reference to active variables such as x increases without bounds, f(x) approaches 1, x , and f(x) 1are avoided. Instead, sets of numbers and their relationship are used to present the , concept throughout, from intuitive examples to definitions. Furthermore, such names as limit at b and limit at-the-right are used for limit as x approaches b and limit as x tends toward infinity. Another innovation, graphs of sequences on n-inverted coordinate systems, has proved to be quite successful in practice. Also, the presentation of a generalized limit not only allows opportunity to unify the concept, but the proof of one generalized limit theorem provides proofs of theorems for six types of familiar limits plus other limits that readers may subsequently encounter.
and lim {(n, sn)} with limsn are used to stress that a limit of a function or sequence has been defined and not a limit of a set of range values. Since students today may not think of a variable as a quantity that changes, reference to active variables such as x increases without bounds, f(x) approaches 1, x , and f(x) 1are avoided. Instead, sets of numbers and their relationship are used to present the , concept throughout, from intuitive examples to definitions. Furthermore, such names as limit at b and limit at-the-right are used for limit as x approaches b and limit as x tends toward infinity. Another innovation, graphs of sequences on n-inverted coordinate systems, has proved to be quite successful in practice. Also, the presentation of a generalized limit not only allows opportunity to unify the concept, but the proof of one generalized limit theorem provides proofs of theorems for six types of familiar limits plus other limits that readers may subsequently encounter.
I wish to express my gratitude and indebtedness to Dr. Bruce E. Meserve for his constructive criticism, guidance, and encouragement during the preparation of the book. Also, thanks are due to Dr. R. G. Smith, Dr. Glen Haddock, to my wife Betty, and to the many others who assisted me in preparing and testing this material.
Donald W. Hight
chapter
Sequences and Their Limits
This book is intended to be read with a pencil in hand. It is not designed .to be read as a story, for unless you knew in advance about limits you would soon be confused and lost. Many examples are given which you should analyze and classify. Questions are asked which you are to ponder and answer for yourself. It will then be possible (let us hope) for you to anticipate subsequent considerations and eventually to grasp for yourself a limit concept and to obtain for yourself acceptable definitions of limits. Now, if you have not already done so, get a pencil in hand and a pad of paper beside your book so that we may start our explorations.
11 Infinite Sequences
You already have some idea of what a sequence is, for the word is common. In referring to a sequence of events you want to communicate that one event happened, then the next, and the next, and so forth. We wish to define an infinite numerical sequence in a similar but more specific manner. To specify that there is a first event and then a next event and a next, and so forth, we utilize the natural numbers (or the set of positive integers). The events that we consider are real numbers and are called terms of the sequence. An infinite sequence of real numbers is a function in which each natural number is associated with a unique real number. Since we are concerned in this text only with infinite sequences of real numbers, we shall refer to them simply as sequences.
We shall express a sequence in a traditional manner as an ordered set or list and also as a set of ordered pairs. Thus a sequence s may be expressed either as a list or ordered set,












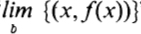 with
with 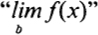 and lim {(n, sn)} with limsn are used to stress that a limit of a function or sequence has been defined and not a limit of a set of range values. Since students today may not think of a variable as a quantity that changes, reference to active variables such as x increases without bounds, f(x) approaches 1, x , and f(x) 1are avoided. Instead, sets of numbers and their relationship are used to present the , concept throughout, from intuitive examples to definitions. Furthermore, such names as limit at b and limit at-the-right are used for limit as x approaches b and limit as x tends toward infinity. Another innovation, graphs of sequences on n-inverted coordinate systems, has proved to be quite successful in practice. Also, the presentation of a generalized limit not only allows opportunity to unify the concept, but the proof of one generalized limit theorem provides proofs of theorems for six types of familiar limits plus other limits that readers may subsequently encounter.
and lim {(n, sn)} with limsn are used to stress that a limit of a function or sequence has been defined and not a limit of a set of range values. Since students today may not think of a variable as a quantity that changes, reference to active variables such as x increases without bounds, f(x) approaches 1, x , and f(x) 1are avoided. Instead, sets of numbers and their relationship are used to present the , concept throughout, from intuitive examples to definitions. Furthermore, such names as limit at b and limit at-the-right are used for limit as x approaches b and limit as x tends toward infinity. Another innovation, graphs of sequences on n-inverted coordinate systems, has proved to be quite successful in practice. Also, the presentation of a generalized limit not only allows opportunity to unify the concept, but the proof of one generalized limit theorem provides proofs of theorems for six types of familiar limits plus other limits that readers may subsequently encounter.