Peter Atkins - Four Laws That Drive the Universe

If you would like to take any of these matters further, then here are some suggestions. I wrote about the conservation of energy and the concept of entropy in my Galileos Finger: The Ten Great Ideas of Science (Oxford University Press, 2003), at about this level but slightly less quantitatively. In The Second Law (W. H. Freeman & Co., 1997) I attempted to demonstrate that laws concepts and implications largely pictorially, inventing a tiny universe where we could see every atom. More serious accounts will be found in my various textbooks. In order of complexity, these are Chemical Principles: The Quest for Insight (with Loretta Jones, W. H. Freeman & Co., 2008), Elements of Physical Chemistry (with Julio de Paula, Oxford University Press and W. H. Freeman & Co., 2006), and Physical Chemistry (with Julio de Paula, Oxford University Press and W. H. Freeman & Co., 2006).

Others, of course, have written wonderfully about the laws. I can direct you to that most authoritative account, Thermodynamics, by G. N. Lewis and M. Randall (McGraw-Hill, 1923; revised by K. S. Pitzer and L. Brewer, 1961). Other useful and reasonably accessible texts on my shelves are The Theory of Thermodynamics, by J. R. Waldram (Cambridge University Press, 1985), Applications of Thermodynamics, by B. D. Wood (Addison-Wesley, 1982), Entropy Analysis, by N. C. Craig (VCH, 1992), Entropy in Relation to Incomplete Knowledge, by K. G. Denbigh and J. S. Denbigh (Cambridge University Press, 1985), and Statistical Mechanics: A Concise Introduction for Chemists, by B. Widom (Cambridge University Press, 2002).

Energy is reported in joules (J): 1 J = 1 kg m2 s2. We could think of 1 J as the energy of a 2 kg ball travelling at 1 m s1. Each pulse of the human heart expends an energy of about 1 J.

The concept of temperature

T he zeroth law is an afterthought. Although it had long been known that such a law was essential to the logical structure of thermodynamics, it was not dignified with a name and number until early in the twentieth century. By then, the first and second laws had become so firmly established that there was no hope of going back and renumbering them. As will become apparent, each law provides an experimental foundation for the introduction of a thermodynamic property. The zeroth law establishes the meaning of what is perhaps the most familiar but is in fact the most enigmatic of these properties: temperature.

Thermodynamics, like much of the rest of science, takes terms with an everyday meaning and sharpens themsome would say, hijacks themso that they take on an exact and unambiguous meaning. We shall see that happening throughout this introduction to thermodynamics. It starts as soon as we enter its doors. The part of the universe that is at the centre of attention in thermodynamics is called the system. A system may be a block of iron, a beaker of water, an engine, a human body. It may even be a circumscribed part of each of those entities. The rest of the universe is called the surroundings. The surroundings are where we stand to make observations on the system and infer its properties. Quite often, the actual surroundings consist of a water bath maintained at constant temperature, but that is a more controllable approximation to the true surroundings, the rest of the world. The system and its surroundings jointly make up the universe. Whereas for us the universe is everything, for a less profligate thermodynamicist it might consist of a beaker of water (the system) immersed in a water bath (the surroundings).

A system is defined by its boundary. If matter can be added to or removed from the system, then it is said to be open. A bucket, or more refinedly an open flask, is an example, because we can just shovel in material. A system with a boundary that is impervious to matter is called closed. A sealed bottle is a closed system. A system with a boundary that is impervious to everything in the sense that the system remains unchanged regardless of anything that happens in the surroundings is called isolated. A stoppered vacuum flask of hot coffee is a good approximation to an isolated system.

The properties of a system depend on the prevailing conditions. For instance, the pressure of a gas depends on the volume it occupies, and we can observe the effect of changing that volume if the system has flexible walls. Flexible walls is best thought of as meaning that the boundary of the system is rigid everywhere except for a patcha pistonthat can move in and out. Think of a bicycle pump with your finger sealing the orifice.

Properties are divided into two classes. An extensive property depends on the quantity of matter in the systemits extent. The mass of a system is an extensive property; so is its volume. Thus, 2 kg of iron occupies twice the volume of 1 kg of iron. An intensive property is independent of the amount of matter present. The temperature (whatever that is) and the density are examples. The temperature of water drawn from a thoroughly stirred hot tank is the same regardless of the size of the sample. The density of iron is 8.9 g cm3 regardless of whether we have a 1 kg block or a 2 kg block. We shall meet many examples of both kinds of property as we unfold thermodynamics and it is helpful to keep the distinction in mind.

*

So much for these slightly dusty definitions. Now we shall use a pistona movable patch in the boundary of a systemto introduce one important concept that will then be the basis for introducing the enigma of temperature and the zeroth law itself.

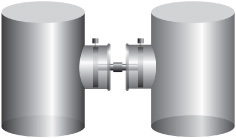
1. If the gases in these two containers are at different pressures, when the pins holding the pistons are released, the pistons move one way or the other until the two pressures are the same. The two systems are then in mechanical equilibrium. If the pressures are the same to begin with, there is no movement of the pistons when the pins are withdrawn, for the two systems are already in mechanical equilibrium.

Suppose we have two closed systems, each with a piston on one side and pinned into place to make a rigid container ( condition arising from the equality of pressures is mechanical equilibrium. Thermodynamicists get very excited, or at least get very interested, when nothing happens, and this condition of equilibrium will grow in importance as we go through the laws.

We need one more aspect of mechanical equilibrium: it will seem trivial at this point, but establishes the analogy that will enable us to introduce the concept of temperature. Suppose the two systems, which we shall call A and B, are in mechanical equilibrium when they are brought together and the pins are released. That is, they have the same pressure. Now suppose we break the link between them and establish a link between system A and a third system, C, equipped with a piston. Suppose we observe no change: we infer that the systems A and C are in mechanical equilibrium and we can go on to say that they have the same pressure. Now suppose we break that link and put system C in mechanical contact with system B. Even without doing the experiment, we know what will happen: nothing. Because systems A and B have the same pressure, and A and C have the same pressure, we can be confident that systems C and B have the same pressure, and that pressure is a universal indicator of mechanical equilibrium.

Now we move from mechanics to thermodynamics and the world of the zeroth law. Suppose that system A has rigid walls made of metal and system B likewise. When we put the two systems in contact, they might undergo some kind of physical change. For instance, their pressures might change or we could see a change in colour through a peephole. In everyday language we would say that heat has flowed from one system to the other and their properties have changed accordingly. Dont imagine, though, that we know what heat is yet: that mystery is an aspect of the first law, and we arent even at the zeroth law yet.