1.1 Computational Intelligence
Computational intelligence is an increasingly important discipline with an impact on more and more domains. It mainly comprises the two large problem classes optimization and machine learning that are strongly connected to each other, but which also cover a broad field of individual problems and tasks. Examples for applications of optimization and learning methods range from robotics to civil engineering. Optimization is the problem of finding optimal parameters for all kinds of systems. Machine learning is an essential part of intelligence. It means that a system is able to recognize structure in data and to predict the future based on past observations from the past. It is therefore related to human learning and thinking. The benefit of learning is the ability to behave reasonable based on experience, in particular considering functional aspects that can be extracted from observations. Machine learning is basically an advancement of statistical methods, a reason why it also denoted as statistical learning.
Traditionally, computational intelligence consists of three main branches: (1) evolutionary algorithms, (2) neural networks, and (3) fuzzy logic. Evolutionary algorithms comprise methods that allow the optimization of parameters of a system oriented to the biological principle of natural evolution. Neural networks are also biologically inspired methods. They are abstract imitations of natural neural information processing. Fuzzy logic allows modeling of linguistic terms with linguistic inaccuracy. Meanwhile, numerous other methods have been developed and influence the three branches of computational intelligence.
1.2 Optimization
Optimization is an important problem class in computer science finding numerous applications in domains like electrical engineering, information management, and many more. Optimization variables may be numerical, discrete, or combinatorial. Moreover, mixed-integer problems contain continuous and discrete variables. A famous combinatorial optimization problem is the traveling salesman problem (TSP) , which is the task to find the shortest tour between a set of cities, which have to be visited. This problem can be arbitrarily difficult. For example, if we consider 100 cities, the number of possible tours exceeds

, which is nearly impossible to compute. The search in this large solution space is a particularly difficult problem. But the world of combinatorial optimization profits from developments in computational complexity. This theory allows differentiating between easy and hard problems. For example, the TSP problem is NP-hard, which means that (probablyto the best of our current knowledge) no algorithm exists that computes a solution in polynomial time.
In this work, we focus on continuous optimization also referred to as numerical optimization. We define an optimization problem as the minimization of an objective function
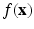
w.r.t. a set of d parameters
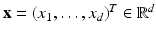
. Every minimization problem can easily be treated as maximization problem by setting
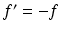
. Figure illustrates the definition of optimality. A local optimum employs the best fitness in its neighborhood, a global optimum employs the best overall fitness. A global optimum is also a (special) local optimum. Optimization methods must prevent getting stuck in local optima.
Fig. 1.1
Illustration of local and global optima of a minimization problem
Some optimization problems are high-dimensional, i.e., a large number of parameters has to be optimized at the same time, while others only concern few variables. High-dimensional optimization problems often occur during computer experiments, when a complex simulation model replaces a lab experiment. The problem that comes up under such conditions is that due to the curse of dimensionality problem no reasonable search in the solution space is possible. In such cases, a stochastic trial-and-error method can yield good results. This also holds for problems that are difficult due to multiple local optima or non-smooth and noisy fitness landscapes.
Many conditions can make an optimization problem difficult to solve:
Often, no analytic expression is available. In this case, it is not possible to apply methods like gradient descent, Newton methods, and other variants.
Problems may suffer from noise, which means that the fitness function evolution of the same candidate solution may result in different fitness values.
Solution spaces may be constrained, i.e., not the whole solution space is feasible. As optima often lie at the constraint boundary, where the success rate drops significantly, heuristics like evolutionary algorithms must be enhanced to cope with changing conditions.
When more than two objectives have to be optimized at the same time, which may be conflictive, a Pareto set of solutions has to be generated. For this sake, evolutionary multi-objective optimization algorithms are a good choice as they naturally work with populations, which allow the evolution of a Pareto set.
Under such conditions classic optimization strategies often fail and heuristics perform good results. Evolutionary algorithms (EAs) are excellent methods to find optima for blackbox optimization problems. EAs are inspired by the natural process of evolution. Different branches began to develop in the mid of the last century. In Germany, Rechenberg and Schwefel [] at the same time. Methods developed in this line of research were called genetic algorithms. All EA research branches have grown together in the recent decade, as similar heuristic extensions can be used and exchanged within different EA types.
1.3 Machine Learning and Big Data
Machine learning allows learning from data. Information is the basis of learning. Environmental sensors, text and image data, time series data in economy, there are numerous examples of information that can be used for learning. There are two different types of learning: supervised and unsupervised. Based on observations, the focus of supervised learning is the recognition of functional relationships between patterns. Labels are used to train a model. Figure illustrates a supervised learning scenario. In classification, a new pattern
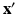
without label information is assigned to a label based on the model that is learned from a training data set. Many effective and efficient machine learning methods have been proposed in the past. Strong machine learning libraries allow their fast application to practical learning problems. Famous methods are nearest neighbor methods, decision trees, random forests, and support vector machines. Deep learning is a class of methods that recently attracts a lot of attention, in particular in image and speech recognition.











 , which is nearly impossible to compute. The search in this large solution space is a particularly difficult problem. But the world of combinatorial optimization profits from developments in computational complexity. This theory allows differentiating between easy and hard problems. For example, the TSP problem is NP-hard, which means that (probablyto the best of our current knowledge) no algorithm exists that computes a solution in polynomial time.
, which is nearly impossible to compute. The search in this large solution space is a particularly difficult problem. But the world of combinatorial optimization profits from developments in computational complexity. This theory allows differentiating between easy and hard problems. For example, the TSP problem is NP-hard, which means that (probablyto the best of our current knowledge) no algorithm exists that computes a solution in polynomial time.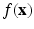 w.r.t. a set of d parameters
w.r.t. a set of d parameters 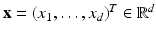 . Every minimization problem can easily be treated as maximization problem by setting
. Every minimization problem can easily be treated as maximization problem by setting 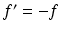 . Figure illustrates the definition of optimality. A local optimum employs the best fitness in its neighborhood, a global optimum employs the best overall fitness. A global optimum is also a (special) local optimum. Optimization methods must prevent getting stuck in local optima.
. Figure illustrates the definition of optimality. A local optimum employs the best fitness in its neighborhood, a global optimum employs the best overall fitness. A global optimum is also a (special) local optimum. Optimization methods must prevent getting stuck in local optima. 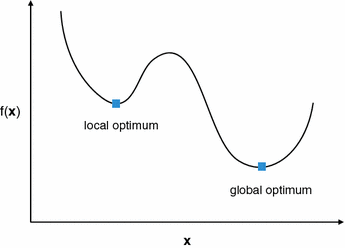
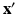 without label information is assigned to a label based on the model that is learned from a training data set. Many effective and efficient machine learning methods have been proposed in the past. Strong machine learning libraries allow their fast application to practical learning problems. Famous methods are nearest neighbor methods, decision trees, random forests, and support vector machines. Deep learning is a class of methods that recently attracts a lot of attention, in particular in image and speech recognition.
without label information is assigned to a label based on the model that is learned from a training data set. Many effective and efficient machine learning methods have been proposed in the past. Strong machine learning libraries allow their fast application to practical learning problems. Famous methods are nearest neighbor methods, decision trees, random forests, and support vector machines. Deep learning is a class of methods that recently attracts a lot of attention, in particular in image and speech recognition.