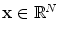1. Introduction
Abstract
Many optimization problems that have to be solved in practice are black box problems. Often, not much is known about an optimization problem except the information one can get via function evaluations. Neither derivatives nor constraints are known. In the worst case, nothing is even known about the characteristics of the fitness function, e.g., whether it is uni- or multimodal.
Many optimization problems that have to be solved in practice are black box problems. Often, not much is known about an optimization problem except the information one can get via function evaluations. Neither derivatives nor constraints are known. In the worst case, nothing is even known about the characteristics of the fitness function, e.g., whether it is uni- or multimodal. This scenario affords the application of specialized optimization strategies often called direct search methods. Evolutionary algorithms that mimic the biological notion of evolution and employ stochastic components to search in the solution space have grown to strong optimization methods. Evolutionary methods that are able to efficiently search in large optimization scenarios and learn from observed patterns in data mining scenarios have found broad acceptance in many disciplines, e.g., civil and electrical engineering. The methods have been influenced from various disciplines: robotics, statistics, computer science, engineering, and the cognitive sciences. This might be the reason for the large variety of techniques that have been developed in the last decades. The employment of computer simulations has become outstandingly successful in engineering within the last years. This development includes the application of optimization and learning techniques in the design and prototype process. Simulations allow the study of prototype characteristics before the product has actually been manufactured. Such a process allows an entirely computed-based optimization of the whole prototype or of its parts and can result in significant speedups and savings of material and money.
Learning and optimization are strongly related to each other. In optimization, one seeks for optimal parameters of a function or system w.r.t. a defined objective. In machine learning, one seeks for an optimal functional model that allows to describe relations between observations. Pattern recognition and machine learning problems also involve solving optimization problems. Many different optimization approaches are employed, from heuristics with stochastic components to exact convex methods.
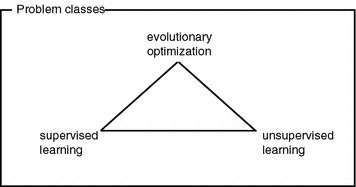
Fig. 1.1
Survey of problem classes the methods in this work belong to: evolutionary optimization, super-, and unsupervised learning
The goal of this book is to give a brief introduction to latest heuristics in evolutionary optimization for continuous solution spaces. The beginning of the work gives a short introduction to the main problem classes of interest: optimization, super-, and unsupervised learning, see Fig.. Optimization is the problem of finding optimal parameters for arbitrary models and functions. Supervised learning is about finding functional models that best model observations with given label information. Unsupervised learning is about learning functional models only based on the structure of the data itself, i.e., without label information. The following three paragraphs give a short introduction to the three problem classes.
1.1 Optimization
Optimization is the search for optimal parameters of a system. The parameters are known as design or objective variables. We assume a set

of solutions that we call solution space or search space. A typical example for a solution space is the set

of continuous values. In most cases, not only one, but many values have to be optimized at the same time resulting in an
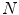
-dimensional search problem, or search problem dimensionality, respectively. For continuous solution spaces, this means we search in
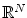
. A famous optimization problem is the traveling salesperson problem. The salesperson has to find the shortest tour through a set of cities and go back to the city, where he started from. In this scenario, a solution consists of a sequence of cities. A feasible solution must contain all cities. Obviously, the solution space has a different structure than the set of continuous solutions. For such solution spaces, special operators have to be employed. We focus on continuous optimization in this book.
Optimality can only be defined w.r.t. some quality measure. We measure the quality of a solution with the help of a quality function
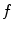
that we also call fitness function. An optimal solution

has a better fitness
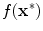
than all other solutions
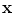
in the solution space
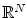
, i.e., for an optimal solution
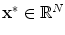
it holds
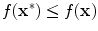
for all
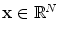
. This definition holds for single-objective optimization problems and has to be extended for multi-objective problems via the concept of Pareto optimality, see Chap.. Without loss of generality, I concentrate on minimization problems. Maximization problems can easily be transformed into minimization problems by inversion of the objective function
A solution
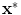
with a better fitness
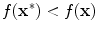
than the solutions in its environment
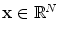














 of solutions that we call solution space or search space. A typical example for a solution space is the set
of solutions that we call solution space or search space. A typical example for a solution space is the set  of continuous values. In most cases, not only one, but many values have to be optimized at the same time resulting in an
of continuous values. In most cases, not only one, but many values have to be optimized at the same time resulting in an 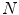 -dimensional search problem, or search problem dimensionality, respectively. For continuous solution spaces, this means we search in
-dimensional search problem, or search problem dimensionality, respectively. For continuous solution spaces, this means we search in 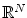 . A famous optimization problem is the traveling salesperson problem. The salesperson has to find the shortest tour through a set of cities and go back to the city, where he started from. In this scenario, a solution consists of a sequence of cities. A feasible solution must contain all cities. Obviously, the solution space has a different structure than the set of continuous solutions. For such solution spaces, special operators have to be employed. We focus on continuous optimization in this book.
. A famous optimization problem is the traveling salesperson problem. The salesperson has to find the shortest tour through a set of cities and go back to the city, where he started from. In this scenario, a solution consists of a sequence of cities. A feasible solution must contain all cities. Obviously, the solution space has a different structure than the set of continuous solutions. For such solution spaces, special operators have to be employed. We focus on continuous optimization in this book.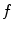 that we also call fitness function. An optimal solution
that we also call fitness function. An optimal solution  has a better fitness
has a better fitness 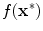 than all other solutions
than all other solutions 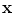 in the solution space
in the solution space 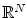 , i.e., for an optimal solution
, i.e., for an optimal solution 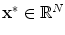 it holds
it holds 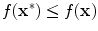 for all
for all 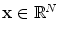 . This definition holds for single-objective optimization problems and has to be extended for multi-objective problems via the concept of Pareto optimality, see Chap.. Without loss of generality, I concentrate on minimization problems. Maximization problems can easily be transformed into minimization problems by inversion of the objective function
. This definition holds for single-objective optimization problems and has to be extended for multi-objective problems via the concept of Pareto optimality, see Chap.. Without loss of generality, I concentrate on minimization problems. Maximization problems can easily be transformed into minimization problems by inversion of the objective function 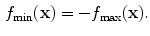
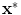 with a better fitness
with a better fitness 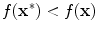 than the solutions in its environment
than the solutions in its environment