Serkan Kiranyaz , Turker Ince and Moncef Gabbouj Adaptation, Learning, and Optimization Multidimensional Particle Swarm Optimization for Machine Learning and Pattern Recognition 2014 10.1007/978-3-642-37846-1_1 Springer-Verlag Berlin Heidelberg 2014
1. Introduction
Abstract
Optimization as a generic term is defined by the Merriam-Webster dictionary as: an act, process, or methodology of making something (as a design, system, or decision) as fully perfect, functional, or effective as possible; specifically: the mathematical procedures (as finding the maximum of a function) involved in this.
Optimization as a generic term is defined by the Merriam-Webster dictionary as: an act, process, or methodology of making something (as a design, system, or decision) as fully perfect, functional, or effective as possible; specifically: the mathematical procedures (as finding the maximum of a function) involved in this.
Dante Aligheiri, around the year 1300, elevated the simple principle of optimization to a virtue:
A number of medieval philosophers and thinkers defended the principle that nature strives for the optimal or the best path. For instance, the famous French mathematician Maupertuis proclaimed: If there occur some changes in nature, the amount of action necessary for this change must be as small as possible. This was also indicated by William of Occam, the most influential philosopher of the fourteenth century, who quoted the principle of Economics as: Entities are not to be multiplied beyond necessity . In science this is best known as: What can be done with fewer is done in vain with more . Above all, optimization is founded and developed by a certain type of ingenious and creative people, the so-called Engineers. As a common misconception, English speakers tend to think that the word engineering is related to the word of engine, thus engineers are people who work with engines. In fact, the word engineer comes from the French word ingnieur which derives from the same Latin roots as the words ingenuity and genius. Therefore, Optimization is the very essence of engineering as engineers (at least the good ones) are not interested with any solution of a given problem, but the best possible or as fully perfect, functional, or effective as possible one. In short, engineering is the art of creating optimum solutions and the optimality therein can be defined by the conditions and constraints of the problem in hand.
The first step of the solution lies in the mathematical modeling of the problem and its constraints. A mathematical model is needed for the proper representation of the variables, features, and constraints. Once the model is formulated in terms of a so-called objective function, then an efficient mathematical optimization technique can be developed to search for the extremum point of the function, which corresponds to the optimum solution of the problem. In mathematical terms, let
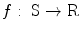
be the objective function from a set S to the real numbers. An optimization technique searches for the extremum point
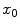
in S such that either
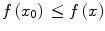
or
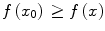
for all x in S . In this way the original problem within which an optimal solution is sought, is transformed to an equivalent (or sometimes approximating) function optimization problem. The original problem can be a multi-objective problem where there is more than one objective present. For example, one might wish to design a video encoder with the lowest possible complexity and highest compression rate. There will be one design with the lowest complexity but possibly with an inferior compression rate and another one with the highest compression rate but possibly with a very high complexity. Obviously, there will be an infinite number of encoders with some compromise of complexity and compression efficiency. As these objectivesusuallyconflict with each other, a trade-off will naturally occur. One way to tackle this kind of problem is to perform a regularization technique, which will properly blend the two or multiple objectives into a single objective function.
1.1 Optimization Era
The optimization era started with the early days of Newton, Lagrange, and Cauchy. Particularly, the development of the mathematical foundations such as differential calculus methods that are capable of moving toward an optimum of a function was possible thanks to the contributions of Newton, Gauss, and Leibnitz to calculus. Cauchy proposed the first steepest descent method to solve unconstrained optimization problems. Furthermore, Bernoulli, Euler, Lagrange, Fermat, and Weistrass developed the foundations of function minimization in calculus while Lagrange invented the method of optimization for constrained problems using the unknown multipliers called after him, i.e., Lagrange multipliers. After the second half of the twentieth century, with the invention of digital computers, massive number of new techniques and algorithms were developed to solve complex optimization problems and such ongoing efforts stimulated further research on different and entirely new areas in optimization era. A major breakthrough was linear programming, which was invented by George Dantzig. To name few other milestones in this area:
Kuhn and Tucker in 1951 carried out studies later leading to the research on Nonlinear programming , which is the general case where the objective function or the constraints or both contain nonlinear parts.
Bellman in 1957 presented the principle of optimality for Dynamic programming with an optimization strategy based on splitting the problem into smaller sub-problems. The equation given by his name describes the relationship between these sub-problems.
Combinatorial optimization is a generic term for a set of optimization methods encapsulating operations research, algorithm theory, and computational complexity theory. Methods in this domain search for a set of feasible solutions in discrete spaces with the goal of finding the optimum solution where exhaustive (or sequential) search is not feasible. It has important applications in several fields, including artificial intelligence, machine learning, mathematics, and software engineering. It is also applied to certain optimization problems that involve uncertainty. For example, many real-world problems almost invariably include some unknown parameters.












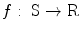 be the objective function from a set S to the real numbers. An optimization technique searches for the extremum point
be the objective function from a set S to the real numbers. An optimization technique searches for the extremum point 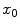 in S such that either
in S such that either 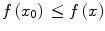 or
or 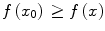 for all x in S . In this way the original problem within which an optimal solution is sought, is transformed to an equivalent (or sometimes approximating) function optimization problem. The original problem can be a multi-objective problem where there is more than one objective present. For example, one might wish to design a video encoder with the lowest possible complexity and highest compression rate. There will be one design with the lowest complexity but possibly with an inferior compression rate and another one with the highest compression rate but possibly with a very high complexity. Obviously, there will be an infinite number of encoders with some compromise of complexity and compression efficiency. As these objectivesusuallyconflict with each other, a trade-off will naturally occur. One way to tackle this kind of problem is to perform a regularization technique, which will properly blend the two or multiple objectives into a single objective function.
for all x in S . In this way the original problem within which an optimal solution is sought, is transformed to an equivalent (or sometimes approximating) function optimization problem. The original problem can be a multi-objective problem where there is more than one objective present. For example, one might wish to design a video encoder with the lowest possible complexity and highest compression rate. There will be one design with the lowest complexity but possibly with an inferior compression rate and another one with the highest compression rate but possibly with a very high complexity. Obviously, there will be an infinite number of encoders with some compromise of complexity and compression efficiency. As these objectivesusuallyconflict with each other, a trade-off will naturally occur. One way to tackle this kind of problem is to perform a regularization technique, which will properly blend the two or multiple objectives into a single objective function.