Euclid - The Thirteen Books of the Elements, Vol. 2

THE THIRTEEN BOOKS OF EUCLIDS ELEMENTS

TRANSLATED FROM THE TEXT OF HEIBERG

WITH INTRODUCTION AND COMMENTARY

BY

SIR THOMAS L. HEATH,

K.C.B., K.C.V.O., F.R.S.,

SC.D. CAMB., HON. D.SC. OXFORD

HONORARY FELLOW (SOMETIME FELLOW) OF TRINITY COLLEGE CAMBRIDGE

SECOND EDITION REVISED WITH ADDITIONS

VOLUME II

BOOKS IIIIX

DOVER PUBLICATIONS, INC.

NEW YORK

This Dover edition, first published in 1956, is an unabridged and unaltered republication of the second edition. It is published through special arrangement with Cambridge University Press.

International Standard Book Number 13: 978-0-486-15819-8

Library of Congress Catalog Card Number: 56-4336

Manufactured in the United States by Courier Corporation

60089027

www.doverpublications.com

BOOK III.

DEFINITIONS.

1. Equal circles are those the diameters of which are equal, or the radii of which are equal.

2. A straight line is said to touch a circle which, meeting the circle and being produced, does not cut the circle.

3. Circles are said to touch one another which, meeting one another, do not cut one another.

4. In a circle straight lines are said to be equally distant from the centre when the perpendiculars drawn to them from the centre are equal.

5. And that straight line is said to be at a greater distance on which the greater perpendicular falls.

6. A segment of a circle is the figure contained by a straight line and a circumference of a circle.

7. An angle of a segment is that contained by a straight line and a circumference of a circle.

8. An angle in a segment is the angle which, when a point is taken on the circumference of the segment and straight lines are joined from it to the extremities of the straight line which is the base of the segment, is contained by the straight lines so joined.

9. And, when the straight lines containing the angle cut off a circumference, the angle is said to stand upon that circumference.

10. A sector of a circle is the figure which, when an angle is constructed at the centre of the circle, is contained by the straight lines containing the angle and the circumference cut off by them.

11. Similar segments of circles are those which admit equal angles, or in which the angles are equal to one another.

D EFINITION 1.

Io v, v a po v, v a v

Many editors have held that this should not have been included among definitions. Some, e.g. Tartaglia, would call it a postulate; others, e.g. Borelli and Playfair, would call it an axiom; others again, as Billingsley and Clavius, while admitting it as a definition, add explanations based on the mode of constructing a circle; Simson and Pfleiderer hold that it is a theorem. I think however that Euclid would have maintained that it is a definition in the proper sense of the term; and certainly it satisfies Aristotles requirement that a definitional statement ( ) should not only state the fact ( ) but should indicate the cause as well (Deanima 11. 2, 413 a 13). The equality of circles with equal radii can of course be proved by superposition, but, as we have seen, Euclid avoided this method wherever he could, and there is nothing technically wrong in saying By equalcircles I mean circles with equal radii. No flaw is thereby introduced into the system of the Elements; for the definition could only be objected to if it could be proved that the equality predicated of the two circles in the definition was not the same thing as the equality predicated of other equal figures in the Elements on the basis of the Congruence-Axiom, and, needless to say, this cannot be proved because it is not true. The existence of equal circles (in the sense of the definition) follows from the existence of equal straight lines and I . Post. 3.

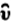
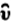
The Greeks had no distinct word for radius, which is with them, as here, the (straightlinedrawn) fromthecentre ( ); and so definitely was the expression appropriated to the radius that was used without the article as a predicate, just as if it were one word. Thus, e.g., in III . I p means for they are radii: cf. Archimedes, OntheSphereandCylinder II . 2, BE 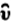..., BEisaradiusofthecircle.

D EFINITION 2.

E , .

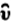
Euclids phraseology here shows the regular distinction between and its compound , the former meaning to meet and the latter to touch. The distinction was generally observed, by Greek geometers from Euclid onwards. There are however exceptions so far as