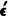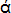BOOK X .
INTRODUCTORY NOTE .We have seen (Vol. ., . of the Elements states that the Pythagoreans were the first to address themselves to the investigation of commensurability, having discovered it by means of their observation of number's. They discovered, the scholium continues, that not all magnitudes have a common measure. "They called all magnitudes measureable by the same measure commensurable, but those which are not subject to the same measure incommensurable, and again such of these as are measured by some other common measure commensurable with one another, and such as are not, incommensurable with the others. And thus by assuming their measures they referred everything to different commensurabilities, but, though they were different, even so (they proved that) not all magnitudes are commensurable with any. (They showed that) all magnitudes can be rational ( 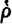 ) and all irrational (
) and all irrational ( 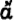 ) in a relative sense (
) in a relative sense ( 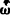 ); hence the commensurable and the incommensurable would be for them natural (kinds) (
); hence the commensurable and the incommensurable would be for them natural (kinds) ( 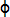
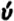
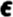 ), while the rational and irrational would rest on assumption or convention (
), while the rational and irrational would rest on assumption or convention ( 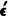
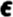 )." The scholium quotes further the legend according to which "the first of the Pythagoreans who made public the investigation of these matters perished in a shipwreck," conjecturing that the authors of this story "perhaps spoke allegorically, hinting that everything irrational and formless is properly concealed, and, if any soul should rashly invade this region of life and lay it open, it would be carried away into the sea of becoming and be overwhelmed by its unresting currents." There would be a reason also for keeping the discovery of irrationals secret for the time in the fact that it rendered unstable so much of the groundwork of geometry as the Pythagoreans had based upon the imperfect theory of proportions which applied only to numbers. We have already, after Tannery, referred to the probability that the discovery of incommensurability must have necessitated a great recasting of the whole fabric of elementary geometry, pending the discovery of the general theory of proportion applicable to incommensurable as well as to commensurable magnitudes.
)." The scholium quotes further the legend according to which "the first of the Pythagoreans who made public the investigation of these matters perished in a shipwreck," conjecturing that the authors of this story "perhaps spoke allegorically, hinting that everything irrational and formless is properly concealed, and, if any soul should rashly invade this region of life and lay it open, it would be carried away into the sea of becoming and be overwhelmed by its unresting currents." There would be a reason also for keeping the discovery of irrationals secret for the time in the fact that it rendered unstable so much of the groundwork of geometry as the Pythagoreans had based upon the imperfect theory of proportions which applied only to numbers. We have already, after Tannery, referred to the probability that the discovery of incommensurability must have necessitated a great recasting of the whole fabric of elementary geometry, pending the discovery of the general theory of proportion applicable to incommensurable as well as to commensurable magnitudes.
It seems certain that it was with reference to the length of the diagonal of a square or the hypotenuse of an isosceles right-angled triangle that the irrational was discovered. Plato ( Theaetetus , 147 D) tells us that Theodorus of Cyrene wrote about square roots ( 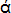
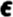 ), proving that the square roots of , 10 were used by the Pythagoreans in direct connexion with this method of approximating to the value of 2. The very method by which Euclid proves these propositions is itself an indication of their connexion with the investigation of 2, since he uses a figure made up of two isosceles right-angled triangles.
), proving that the square roots of , 10 were used by the Pythagoreans in direct connexion with this method of approximating to the value of 2. The very method by which Euclid proves these propositions is itself an indication of their connexion with the investigation of 2, since he uses a figure made up of two isosceles right-angled triangles.
The actual method by which the Pythagoreans proved the incommensurability of 2 with unity was no doubt that referred to by Aristotle ( Anal. prior . , 41a 267), a reductio ad absurdum by which it is proved that, if the diagonal is commensurable with the side, it will follow that the same number is both odd and even. The proof formerly appeared in the texts of Euclid as X . 117, but it is undoubtedly an interpolation, and August and Heiberg accordingly relegate it to an Appendix. It is in substance as follows.
Suppose AC , the diagonal of a square, to be commensurable with AB , its side. Let : be their ratio expressed in the smallest numbers.
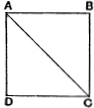
[Eucl. I . 47]
Then > and therefore necessarily > 1.











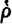 ) and all irrational (
) and all irrational ( 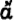 ) in a relative sense (
) in a relative sense (  ); hence the commensurable and the incommensurable would be for them natural (kinds) (
); hence the commensurable and the incommensurable would be for them natural (kinds) ( 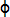
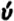
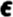 ), while the rational and irrational would rest on assumption or convention (
), while the rational and irrational would rest on assumption or convention (