Allan Clark - Elements of Abstract Algebra

The Greek Alphabet

Symbols for Special Sets

N	natural numbers
N k	{1,2,... , k }
Z	integers
Z n	integers modulo n
	units of Z n
Z( i )	Gaussian integers
Q	rational numbers
R	real numbers
C	complex numbers

A set is any aggregation of objects, called elements of the set. Usually the elements of a set are mathematical quantities of a uniform character. For example, we shall have frequent occasion to consider the set of integers {... , 2, 1, 0, 1, 2,...}, which is customarily denoted Z (for the German Zahlen, which means numbers). We shall use also the set Q of rational numbersnumbers which are the quotient of two integers, such as 7/3, 4/5, 2.

To give an example of another type, we let K denote the set of coordinate points ( x , y ) in the xy -coordinate plane such that x 2 + y 2 = 1. Then K is the circle of unit radius with the origin as center.

To indicate that a particular quantity x is an element of the set S , we write x S , and to indicate that it is not, we write x S. Thus 2 Z , but 1/2 Z ; and 1/2 Q , but 2 Q .

A set is completely determined by its elements. Two sets are equal if and only if they have precisely the same elements . In other words, S = T if and only if x S implies x T and x T implies x S .

It will be convenient to write x , y , z S for x S , y S , and z S .

A set S is a subset of a set T if every element of S is an element of T , or in other words, if x S implies x T . To indicate that S is a subset of T we write S T . If S T and T S , then x S implies x T and x T implies x S , so that S = T .

The empty set is the set with no elements whatever. The empty set is a subset of every set T . If S is a subset of T and neither S = nor S = T , then S is called a proper subset of T .

Frequently a set is formed by taking for its elements all objects which have a specific property. We shall denote the set of all x with the property P by { x P ( x )}. Thus,

Z = { x x is an integer}.

To indicate that a set is formed by selecting from a given set S those elements with property P , we write { x S P ( x )}. It is clear that { x S P ( x )} is always a subset of S . For example, the set of even integers,

2 Z = { x Z x = 2 y , y Z },

is a subset of Z .

The intersection of two sets S and T is the set S T of elements common to both. In other words,

S T = { x x S and x T }.

The intersection S T is a subset of both S and T . The sets S and T are said to be disjoint if S T = .

We note the following properties of intersection:

1. A (B C )= ( A B ) C ,
2. A B = B A ,
3. A A = A and A = ,
4. A B = A if and only if A B .

Let S 1, S 2 ,... , Sn be sets. Then we shall write

as an abbreviation for

S 1 S 2 Sn = { x x Si for each i = 1, 2,... , n }.

The union of two sets S and T is the set S T of elements in S or T or in both S and T . In other words,

S T = { x x S and/or x T }.

S and T are both subsets of S T .

The following properties of union are analogous to those of intersection:

1. A ( B C ) = ( A B ) C ,
2. A B = B A ,
3. A A = A and A = A ,
4. A B = B if and only if A B .

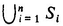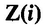
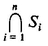
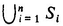Let S 1, S 2,... , Sn be sets. Then we shall write as an abbreviation for