Frédéric Butin - Algebra: Polynomials, Galois Theory and Applications

DOVER PUBLICATIONS, INC.

Mineola, New York

Copyright

Copyright 2017 by Frdric Butin

All rights reserved.

Bibliographical Note

This Dover edition, first published in 2017, is a new English translation of AlgbrePolynmes, thorie de Galois et applications informatiques, published in Paris by Hermann Editeurs in 2011.

Library of Congress Cataloging-in-Publication Data

Names: Butin, Frdric.

Title: Algebra : polynomials, Galois theory and applications / FrdricButin.

Other titles: Algbre. English

Description: Dover edition. | Mineola, New York : Dover Publications, [2017] | Series: Aurora Dover modern math originals | English translation of: Algbre : Polynmes, thorie de Galois et applications informatiques (Paris : Hermann Editeurs, 2011). Includes bibliographical references and index.

Identifiers: LCCN 2016043751| ISBN 9780486810157 | ISBN 0486810151

Subjects: LCSH: Galois theory. | Polynomials. | Algebra, Abstract.

Classification: LCC QA214 .B8813 2017 | DDC 512/.32dc23

LC record available at https://lccn.loc.gov/2016043751

Manufactured in the United States by LSC Communications

810151012017

www.doverpublications.com

Many students are familiar with Galois theory because they have learned that equations of degree greater than or equal to five are not solvable by radicals, or because they have heard about insolvable problems such as the Delian problem, the angle trisection or the quadrature of the circle.

Luckily, Galois theory is not restricted to negative solutions of historical problems! The theory makes many issues easier to understand through the agreement that it establishes between the subfields of a given field and the subgroups of the group of its automorphisms. It is also linked to practical applications such as error-correcting codes that are widely used in digital storage media.

This book is addressed to undergraduate and graduate students, to students who are preparing for a masters degree, and to anyone who wants to discover the properties of this theory. Engineering students will also find a presentation of the mathematical tools underlying the techniques that they use.

The aim of the book is to provide the reader with a clear and precise way to use all the tools needed for their progress (the book is self-contained). The proofs of the theorems and the exercises (they are all entirely solved) are detailed to facilitate understanding. The book is divided into three main parts, as well as a small number of chapters (10), which presents the topics with unity.

The first part introduces the essential notions of Galois theory. It reviews arithmetic, cryptography, and the symmetric group in the first chapter; in the second chapter, rings and polynomials, Euclidean division and the extended algorithm are discussed, as well as multivariate, symmetric, and general polynomials that are irreducible.

The second part is devoted to algebraic, normal and separable extensions, Galois extensions (which are at the center of the theory), followed by abelian, cyclic and radical extensions, as well as cyclotomic polynomials. After completing the second part, the reader will have a good understanding of the Galois group of a polynomial.

Applications of Galois theory are presented in the third part. Ruler and compass constructions are followed by the study of irreducible polynomials over finite fields, their factorization and applicationsparticularly in computer science, where the error-correcting code of CDs is explicitly worked outand results about algebraic integers.

From the beginning of the book, the study takes place in a general framework to provide the reader with a global view of the subject. The goal is not to engage in abstract applications for fun, but to avoid masking the essential point by many supplementary hypotheses due to particular cases. Starting from this general framework, the book always aims for practical applications: therefore, the calculations are entirely worked out, because if the theory seems transparent, this is often due to insight gained by working through the relevant calculations.

Throughout the book we also make use of formal computation: many applications suggest a different and wider view of problems and use a current tool to provide examples that are too tedious to study by hand. The chosen software is Maple, but other software programs can be used.

The book gives several results rarely found in the literature, such as the Chebotarev theorem, the explicit study of error-correcting codes and the irre-ducibility of the permanent.

A biography of quoted mathematicians is located at the end of the book, which enables the reader to examine their mathematical culture.

I am grateful to Gadi S. Perets who helped me greatly with proofreading the English text.

Frdric Butin

Paris, France

Solutions of certain polynomial equations can be written with square roots, cubic roots, fourth roots ... (cf. solutions of equations of degree 2 with the discriminant formula). However, it is well known that equations of degree greater than or equal to 5 cannot, in general, be solved with this type of formula. What is the reason?

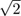Let us consider three examples. First, let us take the equation x2 2 = 0. Its two roots in are and , thus the smallest subfield of containing and the roots of this equation is [], i.e., the set of numbers of the form a + b with (a, b) 2 (in fact we have () and 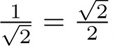). This is a vector space over , and a basis of this space is (1, ).

Let f be an automorphism of the field [] that fixes the elements of . Then we have

and we get two maps f1 and f2 determined by the relations f1() = and f2() = . Conversely, these two maps are automorphisms of []. Then, the group of automorphisms of [