1. Construction of Liouvillian Classes of Functions and Liouvilles Theory
Some algebraic and differential equations are explicitly solvable. What does this mean? If an explicit solution is presented, the question answers itself. However, in most cases, every attempt to solve an equation explicitly is doomed to failure. We are then tempted to prove that certain equations have no explicit solutions. It is now necessary to define exactly what we mean by explicit solutions (otherwise, it is unclear what we are trying to prove).
From the modern viewpoint, the classical works on the subject lack rigorous definitions and statements of theorems. Nonetheless, it is clear that Liouville understood exactly what he was proving. He not only stated the problems on solvability of equations by elementary functions and by quadratures, but he also algebraized them. His work made it possible to define all such notions over an arbitrary differential field. But the standards of mathematical rigor were different in the time of Liouville. Indeed, according to Kolchin [], even Picard failed to give accurate, unambiguous definitions. Kolchins work satisfies modern standards, but his definitions are given for abstract differential fields from the very beginning.
However, the indefinite integral of an elementary function and the solution of a linear differential equation are functions rather than elements of an abstract differential field. In function spaces, for example, apart from differentiation and algebraic operations, an absolutely nonalgebraic operation is defined, namely composition. Anyhow, function spaces provide greater means for writing explicit formulas than abstract differential fields. Moreover, we should take into account that functions can be multivalued, can have singularities, and so on.
In function spaces, it is not hard to formalize the problem of unsolvability of equations in explicit form, and in this book, we are interested in this particular problem. One can proceed as follows: fix a class of functions and say that an equation is solvable explicitly if its solution belongs to this class. Different classes of functions correspond to different notions of solvability.
1.1 Defining Classes of Functions by Lists of Basic Functions and Admissible Operations
A class of functions can be introduced by specifying a list of basic functions and a list of admissible operations . Given these two lists, the class of functions is defined as the set of all functions that can be obtained from the basic functions by repeated application of admissible operations. In Sect., we define Liouvillian classes of functions in exactly this way.
Liouvillian classes of functions, which appear in problems of solvability in finite terms, contain multivalued functions. Thus the basic terminology should be made clear. In this section, we work with multivalued functions globally, which leads to a more general understanding of classes of functions defined by lists of basic functions and admissible operations. In this global version, a multivalued function is regarded as a single entity, and we can define operations on multivalued functions .
The result of such an operation is a set of multivalued functions; every element of this set is referred to as a function obtained from the given functions by the given operation. The class of functions is defined as the set of all (multivalued) functions that can be obtained from the basic functions by repeated application of admissible operations.
Let us define, for example, the sum of two multivalued functions of one variable.
Definition 1.1
Take an arbitrary point a on the complex line, a germ f a of an analytic function f at the point a , and a germ g a of an analytic function g at the same point a . We say that the multivalued function
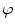
generated by the germ
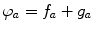
is representable as the sum of the functions f and g .
For example, it is easy to see that exactly two functions are representable in the form
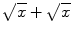
, namely,
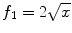
and f 20. Other operations on multivalued functions are defined in exactly the same way. For a class of multivalued functions, being stable under addition means that together with any pair of its functions, this class contains all functions representable as their sum. The same applies to all other operations on multivalued functions understood in the same sense asabove.
In the definition given above, it is not only the operation of addition that plays a key role but also the operation of analytic continuation hidden in the notion of multivalued function. Indeed, consider the following example. Let f 1 be an analytic function defined on an open subset U of the complex line
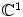
and admitting no analytic continuation outside of U , and let f 2 be an analytic function on U given by the formula
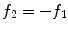
. According to our definition, the zero function is representable in the form f 1 + f 2 on the entire complex line . From the commonly accepted viewpoint, the equality
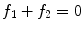
holds inside the region U but not outside.
In working with multivalued functions globally, we do not insist on the existence of a common region where all necessary operations would be performed on single-valued branches of multivalued functions. A first operation can be performed in a first region, then a second operation can be performed in a second, different, region on analytic continuations of functions obtained in the first step. In essence, this more general understanding of operations is equivalent to including analytic continuation in the list of admissible operations on analytic germs. For functions of a single variable, it is possible to obtain topological obstructions even with this more general understanding of operations on multivalued analytic functions.
In the sequel, in considering topological obstructions to the membership of an analytic function of a single variable in a certain class, we will always mean this global definition of the function class via lists of basic functions and admissible operations.
For functions of several variables, things do not work in this general setting, and we are forced to adopt a more restrictive formulation (see Sect., in which we deal with multivariable functions.
1.2 Liouvillian Classes of Functions of a Single Variable
In this section, we define Liouvillian classes of functions of a single variable (for the multivariable case, the corresponding definitions are given in Chap.). We will describe these classes by lists of basic functions and admissible operations.











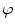 generated by the germ
generated by the germ 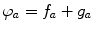 is representable as the sum of the functions f and g .
is representable as the sum of the functions f and g .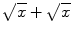 , namely,
, namely, 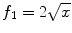 and f 20. Other operations on multivalued functions are defined in exactly the same way. For a class of multivalued functions, being stable under addition means that together with any pair of its functions, this class contains all functions representable as their sum. The same applies to all other operations on multivalued functions understood in the same sense asabove.
and f 20. Other operations on multivalued functions are defined in exactly the same way. For a class of multivalued functions, being stable under addition means that together with any pair of its functions, this class contains all functions representable as their sum. The same applies to all other operations on multivalued functions understood in the same sense asabove.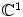 and admitting no analytic continuation outside of U , and let f 2 be an analytic function on U given by the formula
and admitting no analytic continuation outside of U , and let f 2 be an analytic function on U given by the formula 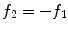 . According to our definition, the zero function is representable in the form f 1 + f 2 on the entire complex line . From the commonly accepted viewpoint, the equality
. According to our definition, the zero function is representable in the form f 1 + f 2 on the entire complex line . From the commonly accepted viewpoint, the equality 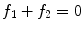 holds inside the region U but not outside.
holds inside the region U but not outside.