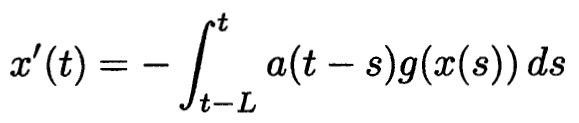T. A. Burton - Stability by Fixed Point Theory for Functional Differential Equations

Stability by Fixed Point Theory for Functional Differential Equations

T. A. Burton

Copyright

Copyright 2006 by Theodore Allen Burton

All rights reserved.

Bibliographical Note

Stability by Fixed Point Theory for Functional Differential Equations is a new work, first published by Dover Publications, Inc., in 2006.

Library of Congress Cataloging-in-Publication Data

Burton, T. A. (Theodore Allen), 1935

Stability by fixed point theory for functional differential equations / T.A. Burton.

p. cm.

Includes bibliographical references and index.

9780486153322

1. Functional differential equationsNumerical solutions. 2. Stability. 3. Fixed point theory. I. Title.

QA372.B879 2006

518.6dc22

2006047426

Manufactured in the United States of America

Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y 11501

To Professor V. Lakshmikantham

Chapter 0

Introduction and Overview

It has long been our view that Liapunovs direct method is the leading technique for dealing with stability problems in many areas of differential equations. We have contributed to that theory for more than forty years and continue to do so. Yet, numerous difficulties with the theory and application to specific problems persist and it does seem that new methods are needed to address those difficulties. There is, of course, the problem of constructing appropriate Liapunov functionals and in carrying out various calculations such as is seen in the annulus argument. These are things which we feel we can overcome with work and imagination. But there are also problems with the types of conditions which are typically imposed on the functions in the differential equations. These conditions are virtually always precise pointwise requirements. Real-world problems with all their uncertainties call for conditions which are averages. In this book we explore the use of fixed point theory in meeting some of those problems.

Not only do the fixed point conditions emerge as averages, but very recently John Appleby has shown that the fixed point methods will also admit stochastic perturbations. In Section 7.3 he discusses how these perturbations relate to real-world applications. Chapter 7 is entirely his contribution. He introduces basic stochastic theory and shows how the fixed point methods yield stability results under stochastic perturbations. Thus, in two ways the fixed point methods seem more applicable to real-world problems than does Liapunovs method.

There is an added benefit to studying stability by fixed point methods. In the next section we illustrate how very complete, simple, and rigorous stability analysis of a highly sophisticated problem can be given using only a complete metric space, the contraction mapping theorem, and the elementary variation of parameters formula. In one step we prove existence, uniqueness, and boundedness of solutions of a problem which has challenged investigators for decades. This is important for students and investigators who are not primarily stability analysts, but whose work leads them to sophisticated stability problems. Increasingly, stability problems emerge in biology, economics, and unlikely places. These problems can often be solved using fixed point theory in an elementary and mathematically honest manner. What is required is imagination in setting up a fixed point mapping. This book is a guide to the process.

For a long time we have been interested in the use of fixed point theory in conjunction with Liapunovs direct method. Fixed point theory can be used directly to study a differential equation when solutions are being considered on a finite interval. But when we are discussing solutions on an infinite interval, some technique seems to be necessary to keep control of the solution. In Burton (1984) we use Liapunov functionals in conjunction with Browders fixed point theorem to obtain periodic solutions of nonlinear functional differential equations. In Burton (1985) a large part of the monograph is devoted to the use of Liapunov functionals with Horns fixed point theorem to obtain periodic solutions. In Burton (1994) we use mildly unbounded Liapunov functionals with Schaefers fixed point theorem to prove global existence for a variety of equations. In a parallel way Seiji (1989) and others have used Liapunov functions with fixed point theory to prove stability. In a different vein, Serban (2001) has used fixed point theory to prove asymptotic stability for a difference equation.

In 1997 several investigators began a systematic study toward a comprehensive stability method based on fixed point theory. As it developed it became more of an investigation into what could be said about classical problems which had offered resistance to Liapunovs direct method and what kinds of absolutely new properties can be discovered. The accent has been on using averaging techniques associated with variation of parameters to avoid pointwise conditions generated by the direct method. In several places we use Liapunovs direct method, but in different ways than described above. First, it is used as a contrast with fixed point methods. Next, we frequently use the direct method to prove that solutions can be continued for all future time. Finally, in one of our sections fixed point methods are used to identify harmless perturbations, while Liapunov functionals are then used to obtain new stability results.

In this book we offer a large collection of examples worked in great detail which clearly establish fixed point theory as a viable tool in stability theory. We also present stability results of types not seen before in the literature which emerge because of the fixed point theory. There are other avenues for investigation and we believe that this can be a major area of research for many years. Moreover, there is such a wide class of problems that this book should serve as a handbook for investigation into the stability properties of specific problems confronting biologists, chemists, economists, engineers, mathematicians, physicists, and other scientists.

During the past year we have had the opportunity to lecture in several countries on fixed point methods in stability. The following material has emerged as what we believe is an informative introduction to the need for the method, the basic techniques, and some convincing examples.

Functional differential equations are often used to model real-world problems in which there are great uncertainties. Yet, our conditions frequently demand excessively precise and detailed conditions which are totally unverifiable. A concrete example of this begins with Volterra (1928) who sought to model a certain biological problem by means of the equation

(0.2.1)

in which xg(x) > 0 if x 0, L > 0, and a(t) is twice differentiable with a(t) not identically zero. He was interested in conditions to ensure that solutions tend to zero as t . At the time he suggested an idea for constructing a Liapunov functional which might yield some stability properties. While that construction was a long time in coming, interest in the formulation of the problem continues to this day. Ergen (1954) and others used the equation to model a circulating fuel nuclear reactor. It is used as a model of one-dimensional viscoelasticity. And it has been used to model neural networks as well as many other problems. Levin (1963) followed Volterras suggestion and successfully constructed a Liapunov functional for a companion equation; thus, we call (0.2.1) the Volterra-Levin equation. The next year, Levin and Nohel (1964) extended that Liapunov functional to the case of (0.2.1), itself. Here is their result.