Nash - Elements of Statistical Thermodynamics.
Here you can read online Nash - Elements of Statistical Thermodynamics. full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Mineola, New York, year: 2006, publisher: Dover Publications, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Elements of Statistical Thermodynamics.
- Author:
- Publisher:Dover Publications
- Genre:
- Year:2006
- City:Mineola, New York
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
- 60
- 1
- 2
- 3
- 4
- 5
Elements of Statistical Thermodynamics.: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Elements of Statistical Thermodynamics." wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Nash: author's other books
Who wrote Elements of Statistical Thermodynamics.? Find out the surname, the name of the author of the book and a list of all author's works by series.
Elements of Statistical Thermodynamics. — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Elements of Statistical Thermodynamics." online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:

I am obliged to the publishers cited below for permission to reproduce a number of figures taken from copyrighted works. As identified by the numbers assigned them in this book, the figures in question are:
, taken from p. 55 of J. D. Fasts Entropy (Eindhoven, Holland: Philips Technical Library, 1962);
, from p. 68 of G. W. Castellans Physical Chemistry , 2nd ed. (Reading, Mass.: Addison-Wesley Publishing Co., 1971);
, from an article by R. K. Fitzgerel and F. H. Verhoek, Journal of Chemical Education 37, 547 (1960);
, from p. 142 of Malcolm Doles Introduction to Statistical Thermodynamics (Englewood Cliffs, N.J.: Prentice-Hall, 1954);
, from pp. 203 and 257 respectively of Statistical Thermodynamics by J. F. Lee, F. W. Sears, and D. L. Turcotte (Reading, Mass.: Addison-Wesley Publishing Co., 1963); and
, from p. 102 of Statistical Thermodynamics by R. H. Fowler and E. A. Guggenheim (Cambridge: University Press, 1939).
I am happy to acknowledge that my first 18 pages have been developed on a pattern suggested by reading of the late Ronald W. Gurneys ingenious introductory text. The arguments on pp. 49 53 and 61 62 owe some of their shape to constructive criticisms of the first edition forwarded to me by William C. Child, Jr., who has kindly supplied several more comments on a draft of this second edition. For a multitude of additional suggestions I am much indebted to Francis T. Bonner, Peter C. Jordan, and Lawrence C. Krisher. To Walter Kauzmann, the author of a splendid alternative to the present text, I am deeply grateful for his generous willingness to indicate many possible improvements. To my wife, Ava Byer Nash, I am beholden not merely for assistance with page-proofs but also for the life-support system that has sustained me throughout. All the foregoing have helped to make this book better than it could otherwise have been. Sole responsibility for any residual blemishes rests with the author, who will welcome any communications making known to him the error(s) of his ways.
Plancks constant, h = 6.626 10 27 erg-sec
Boltzmann constant, k = 1.381 10 16 erg/K
Avogadros number, N = 6.023 1023 mole 1
Gas-law constant, R = 8.314 107 ergs/mole-K
= 1.987 cal/mole-K
The game of checkers is played on an array of 32 squares distinguished by their geometric placement. Consider a game that has reached a stage at which Black has 4 men and 4 kings while Red also has 4 men and 4 kings. Noting that the different kinds of counters (e.g., red man and red king, or red king and black king) are readily distinguishable from each other, but that counters of the same sort (e.g., the 4 red men) are not thus distinguishable, determine the number of recognizably different positions possible at this stage of the game.
a) Show that, in five-card stud poker, the number of possible five-card hands is
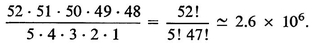
b) Consider the probability that, in a game of five-card stud, you will be dealt a flush (i.e., five cards of the same suit). By showing that the number of ways in which you may be dealt a flush is
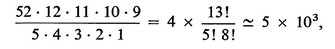
demonstrate that your chance of being dealt a flush is of the order of 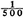 .
.
a) In draw poker there is about a 49% chance that a randomly dealt five-card hand will contain at least two cards of the same denomination. This conclusion is perhaps most readily demonstrated by showing that the probability that the hand does not contain two cards of the same denomination is given by the expression
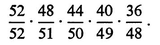
Justify this expression, and complete the indicated demonstration.
b) In a class of 50 randomly selected students, what is the probability that two will have the same birthday? This surprisingly large probability is easily obtained by adapting the development in part (a) to calculate the probability that two students will not have the same birthday.
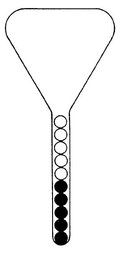
[After Sussman, J. Chem. Educ. , 49 (1963).] a) In the neck of the sealed flask shown below, 5 white balls rest on top of 5 black balls. Suppose that the balls are tipped into the body of the flask, and that the flask is well shaken and then returned to the inverted position shown here. Demonstrate that the probability that the indicated arrangement will again turn up is
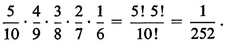
b) What is the physical significance of the function 10!/5! 5!?
c) Determine the number of distinguishable arrangements that would be possible if all ten balls were differently colored.
a) The total number of miscrostates () associated with all configurations possible when N distinguishable harmonic oscillators share Q energy quanta is:
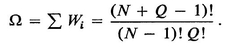
To derive this formula, we symbolize each of the oscillators by an o , each of the quanta by a u . At the left end of a line we set down one o , and then consider in how many ways we can follow the one o , on the same line, with the remaining (N 1) o s and the Q u s. Conceiving each o as possessing all u s appearing to its right prior to the appearance of the next o , we see that the total number of permutations possible will also represent the total number of possible microstates (). Justify this statement, and derive the above formula.
b) Use the formula to confirm the statement made in the text that 2002 distinct microstates are possible when 10 oscillators share 5 energy quanta.
c) Use the formula, and Stirlings approximation, to confirm that 1000 oscillators sharing 1000 energy quanta can assume a total in the order of 10600 microstates.
a) Justify the claim that the formula W = N !/( H !)( T !) yields the number of ways ( W ) in which some particular numbers of heads ( H ) and tails ( T ) can be produced in a series of N tosses of a well-balanced coin.
b) For a series of 1000 tosses of a coin, we define A = W H T /W 500 500, where, W500500 is the number of microstates associated with the predominant configuration, and W H T is the number of microstates associated with the configuration characterized by some particular numbers of heads ( H ) and tails ( T ). Show that log A = 1000 log 500 H log H T log T .
c) Using the formula noted in (b), show that a 400-600 configuration possesses only about 10 9 as many microstates as the predominant 500-500 configuration.
d) Amending the formula in (b) as required for a series of 100 tosses, show that the 40-60 configuration has (as indicated in ) approximately 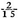
Font size:
Interval:
Bookmark:
Similar books «Elements of Statistical Thermodynamics.»
Look at similar books to Elements of Statistical Thermodynamics.. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Elements of Statistical Thermodynamics. and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.


















