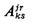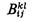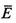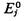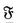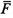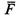Wolfgang Yourgrau - Treatise on Irreversible and Statistical Thermodynamics: An Introduction to Nonclassical Thermodynamics

This Dover edition is dedicated to the memory of
Professor Wolfgang Yourgrau.

Copyright Copyright 1966, 1982 by Thella Yourgrau, Alwyn van der Merwe and Gough Raw

All rights reserved under Pan American and International Copyright Conventions.

Published in Canada by General Publishing Company, Ltd., 895 Don Mills Road, 400-2 Park Centre, Toronto, Ontario M3C 1W3.

Published in the United Kingdom by David & Charles, Brunel House, Forde Close, Newton Abbot, Devon TQ12 4PU.

Bibliographical Note

This Dover edition, first published in 1982 and republished in 2002, is an unabridged and extensively corrected republication of the work originally published by The Macmillan Company, N.Y, 1966.

Library of Congress Cataloging-in-Publication Data

Yourgrau, Wolfgang.
Treatise on irreversible and statistical thermophysics.
Reprint. Originally published: New York: Macmillan, 1966.
Includes bibliographies and index.

9780486151090

1. Irreversible processes. 2. Statistical thermodynamics. I. Van der Merwe,
Alwyn. II. Raw, Gough. III. Title.
[QC318.I7Y68 1982]
530.12
81-19450
AACR2

Manufactured in the United States of America
Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y 11501

Dedicated
to the memory of
Erwin Schrdinger

PREFACE

The revolutionary triumphs of quantum theory and relativity theory, as well as the startling results of elementary particle physics, have dramatically changed our picture of physical reality. It cannot be gainsaid that these areas of physics treat the grand and sublime and therefore enjoy a privileged position within the natural sciences. Needless to say, there is nothing deplorable in this state of affairs.

However, our interest in thermophysics can never remain marginal. First of all, a thorough study of physico-chemical systems must take into account their temperature and entropy, in addition to their nonthermal parameters. Secondly, thermophysics poses one of the most exciting questions in theoretical physics: how can one reconcile the irreversibility of natural processes with the reversible mechanics governing the elementary constituents of thermal systems?

The term thermophysics was proposed by Guggenheim, and strongly advocated by R. J. Seeger, as being the most appropriate to describe the science that examines the connection of temperature and entropy with the nonthermal properties of matter and radiation. Some authors have extended the conventional meaning of thermodynamics to connote the very same science. Although in the subtitle of this book we make a concession to this rather ambiguous practice, in our text we follow the stricter tradition. Hence, thermodynamics without qualification, denotes solely the phenomenological part of thermophysics. It should be noted that this term refers generally to dynamic situations. We have adopted this interpretation, at least in Chapter 1. In other words, we do not arbitrarily limit ourselves to a discussion of systems in thermomechanical and chemical equilibrium and to hypothetical processes involving such statesas is frequently done in literature. We believe, along with some other authors, that such a restricted form of thermodynamics could better be designated as thermostatics.

Thermophysics is naturally subdivided into two parts: phenomenological thermophysics and statistical thermophysics. The former discipline deals directly with the macroscopic or bulk properties of any thermophysical system, while the latter is concerned with these in terms of the statistical-mechanical laws that determine the behavior of the microscopic or atomic constituents of the system.

We might finally explain how we interpret the qualification classical. When applied to thermophysics, the term excludes the whole of statistical mechanics, while in the phenomenological domain it includes only thermostatics. The axiomatic foundation of classical theory thus rests upon the zeroth, first, second, and third laws of thermodynamics and encompasses mainly equilibrium situations and reversible processes.

We wish to acknowledge our indebtedness to Professors W. M. Elsasser (Princeton), S. Mandelstam (Berkeley), L. Onsager (Yale), and M. J. Stephen (Yale) for their critical reading of different parts of the manuscript. Invaluable suggestions were also offered by Professors J. Bardeen (Illinois) and P. G. Bergmann (Syracuse), Dr. D. Gray, and Professors M. J. Klein (Case Institute of Technology) and A. Land (Ohio State). We have further benefited from the very helpful advice of Professor L. Rosenfeld (Nordita) and are extremely grateful to Professor W. Heisenberg (Max-Planck-Institut fr Physik) for his incisive evaluation of the completed manuscript.

At the end of each chapter we have listed the most essential papers and books consulted. Our appreciation for the indispensable aid derived from these sources should not go unmentioned.

W. Yourgrau
A. van der Merwe
G. Raw

Table of Contents

GLOSSARY OF SYMBOLS AND PHYSICAL CONSTANTS

GLOSSARY OF SYMBOLS

A	area
A	chemical affinity
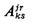	probability of transition from state jr to state ks
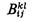	coefficient in the collision number hypothesis
C p	heat capacity at constant pressure
C v	heat capacity at constant volume
D	degree of gas degeneration
D ( y )	Debye function with argument y
D	operator defined in Eq. (55), Chapter 4
E	energy of macroscopic system
E	Youngs modulus
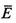	average energy of isothermal system
E *	energy of supersystem
E j	energy eigenvalue of macroscopic system
E k	kinetic energy
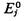	eigenvalue of H
F	Helmholtz free energy
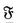	Faraday constant
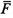	phase, or ensemble, average of function F ( q , p )
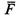	time average of function F ( q , p )
phase average of function F ( q , p )
F i	Onsager force
F s ()	function defined in Eq. (115), Chapter 3
F D ( y )	function ( y /3) D ( y )
G	Gibbs free energy
H	enthalpy
H	Hamiltonian function
H	Hamiltonian operator
H B	Boltzmanns H -function
H	unperturbed Hamiltonian
H	perturbation on H
H*	quantum-mechanical H -function
equilibrium value of H*
I	electrical current
I	moment of inertia of rotator
I	value of moment of inertia I for r = r
J	magnitude of J e
J	magnitude of J
J	quantum number determining magnitude of J