 First eBook publication October 2018. Text Copyright 2018, 2009, 2001 by Kaplan Inc. All rights reserved. No part of this book may be reproduced or distributed in any form or by any means without the written permission of the copyright owner. Published by Barrons Educational Series, Inc. 750 Third Avenue New York, NY 10017 www.barronseduc.com Print edition ISBN: 978-1-4380-1039-7
First eBook publication October 2018. Text Copyright 2018, 2009, 2001 by Kaplan Inc. All rights reserved. No part of this book may be reproduced or distributed in any form or by any means without the written permission of the copyright owner. Published by Barrons Educational Series, Inc. 750 Third Avenue New York, NY 10017 www.barronseduc.com Print edition ISBN: 978-1-4380-1039-7
eISBN: 978-1-4380-6528-1 CONTENTS This book is designed to make geometry painless.
It has several unique features to help you both enjoy geometry and excel at it. Experiments The book contains a series of experiments designed to help deepen your understanding of geometry. If you do the experiments, you will gain an intuitive understanding of geometry. Why not try some of the experiments? They are fun and informative. Painless steps  Complex procedures are divided into a series of painless steps. These painless steps help you solve problems in a systematic way.
Complex procedures are divided into a series of painless steps. These painless steps help you solve problems in a systematic way.
Just follow the steps one at a time, and youll be able to solve most geometry problems. Examples Most problems are illustrated with an example. Study each of the examples. If you are in trouble, copy the example and learn it. Research shows that writing /copying the problem and the solution may help you understand it. Illustrations Painless Geometry is full of illustrations to help you better understand geometry.
Geometry is a visual subject. Its important for you to draw the problems and examples, too. If you can visualize a problem, it will be easier to understand it. CautionMajor mistake territory Occasionally you will find boxes entitled CautionMajor Mistake Territory. These boxes will help you avoid common pitfalls. Be sure to read them carefully.
Study strategies  Occasionally you will see sections called Study Strategies. Here you will find tips on how to study the material in a particular section that are guaranteed to improve your performance. Mini-proofs
Occasionally you will see sections called Study Strategies. Here you will find tips on how to study the material in a particular section that are guaranteed to improve your performance. Mini-proofs  Numerous mini-proofs appear throughout the book. Written informally, these mini-proofs are the first step toward understanding formal geometry proofs. Brain ticklers There are three or four problems after each section of the book. These exercises are designed to make sure that you understand what you just learned.
Numerous mini-proofs appear throughout the book. Written informally, these mini-proofs are the first step toward understanding formal geometry proofs. Brain ticklers There are three or four problems after each section of the book. These exercises are designed to make sure that you understand what you just learned.
Complete all the Brain Ticklers. If you get any wrong, go back and study the materials and examples before it. Super brain ticklers At the end of each chapter are Super Brain Ticklers, which will review all the material in the chapter. Solve these problems to make sure that you understand each chapter. Dont move forward to the next chapter of the book until you really understand what was in the last chapter. Geometry is a linear subject, and what you dont know in one chapter will haunt you in the next.
Dont move forward if any topic confuses you. Go back and try to figure out what you dont know. Geometry can be painless, so why not get started? is titled A Painless Beginning, and it really is. It is an introduction to the basic terms and symbols of geometry. , Angles, will teach you everything about angles. , Parallel and Perpendicular Lines, will show you how to identify parallel and perpendicular lines. , Parallel and Perpendicular Lines, will show you how to identify parallel and perpendicular lines.
You will learn what types of angles are formed when parallel and perpendicular lines are formed. , Triangles, shows you that there is more to learn about triangles than you ever dreamed possible. You will learn the types of triangles, as well as how to find the perimeter and area of a triangle. , Similar and Congruent Triangles, explains what similar and congruent triangles are. By the time you finish reading this chapter, you will know what SSS, SAS, ASA, and AAS mean and how to use each of them to prove that two triangles are congruent. is titled Quadrilaterals, which is a fancy word for four-sided figures.
Trapezoids, parallelograms, rhombuses, rectangles, and squares are all quadrilaterals. You will learn all about these interesting polygons here. is titled Polygons and you will learn that polygons are everywhere. The frame of your television is a polygon and so is the STOP sign down the street. You will be able to impress your friends when you know the names of your polygons, and youll learn the fascinating things all regular polygons have in common. could have been titled Circles, Circles, and More Circles.
You may know what a circle is, but you will find out how a pie is not only something you eat but an essential term in geometry. , Perimeter, Area, and Volume, will show you how to find the perimeter, area, and volume of some common and not so common shapes. Its painless, just watch. , Graphing, will teach you how to graph a point and a line. You can use what you learn here to draw your own geometric shapes. pencil.
When youre ready for a break, use these same tools to create some interesting designs. If you are learning geometry for the first time, or if you are trying to remember what you learned but forgot, this book is for you. It is a painless introduction to geometry that is both fun and instructive. Dive inand remember, its painless! Geometry is a mathematical subject, but it is just like a foreign language. In geometry you have to learn a whole new way of looking at the world. There are hundreds of terms in geometry that youve probably never heard before.
Geometry also uses many common terms, but they have different meanings. A point is no longer the point of a pencil, and a plane is not something that flies in the sky. To master geometry you have to master these familiar and not so familiar terms, as well as the theorems and postulates that are the building blocks of geometry. You have a big job in front of you, but if you follow the step-by-step approach in this book and do all the experiments, it can be painless. Undefined terms are terms that are so basic they cannot be defined, but they can be described. A point is an undefined term.
A point is a specific place in space. A point has no dimension. It has no length, width, or depth. A point is represented by placing a dot on a piece of paper. A point is labeled by a single capital letter. 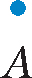 A line is a set of continuous points that extend indefinitely in either direction.
A line is a set of continuous points that extend indefinitely in either direction.
In this book, the term line will always mean a straight line.  This line is called line AB , or line AC , or line BC , or
This line is called line AB , or line AC , or line BC , or 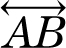 ,
, 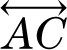 , or
, or 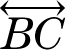 . The two-ended arrow over the letters tells you that the letters are describing a line. You can name a line by any two points that lie on the line. A plane is a third undefined term. A plane is a flat surface that extends infinitely in all directions.
. The two-ended arrow over the letters tells you that the letters are describing a line. You can name a line by any two points that lie on the line. A plane is a third undefined term. A plane is a flat surface that extends infinitely in all directions.
If you were to imagine a table-top that went in every direction forever, you would have a plane. 
Next page













 First eBook publication October 2018. Text Copyright 2018, 2009, 2001 by Kaplan Inc. All rights reserved. No part of this book may be reproduced or distributed in any form or by any means without the written permission of the copyright owner. Published by Barrons Educational Series, Inc. 750 Third Avenue New York, NY 10017 www.barronseduc.com Print edition ISBN: 978-1-4380-1039-7
First eBook publication October 2018. Text Copyright 2018, 2009, 2001 by Kaplan Inc. All rights reserved. No part of this book may be reproduced or distributed in any form or by any means without the written permission of the copyright owner. Published by Barrons Educational Series, Inc. 750 Third Avenue New York, NY 10017 www.barronseduc.com Print edition ISBN: 978-1-4380-1039-7 Complex procedures are divided into a series of painless steps. These painless steps help you solve problems in a systematic way.
Complex procedures are divided into a series of painless steps. These painless steps help you solve problems in a systematic way. Occasionally you will see sections called Study Strategies. Here you will find tips on how to study the material in a particular section that are guaranteed to improve your performance. Mini-proofs
Occasionally you will see sections called Study Strategies. Here you will find tips on how to study the material in a particular section that are guaranteed to improve your performance. Mini-proofs  Numerous mini-proofs appear throughout the book. Written informally, these mini-proofs are the first step toward understanding formal geometry proofs. Brain ticklers There are three or four problems after each section of the book. These exercises are designed to make sure that you understand what you just learned.
Numerous mini-proofs appear throughout the book. Written informally, these mini-proofs are the first step toward understanding formal geometry proofs. Brain ticklers There are three or four problems after each section of the book. These exercises are designed to make sure that you understand what you just learned.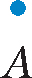 A line is a set of continuous points that extend indefinitely in either direction.
A line is a set of continuous points that extend indefinitely in either direction. This line is called line AB , or line AC , or line BC , or
This line is called line AB , or line AC , or line BC , or 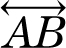 ,
, 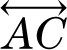 , or
, or 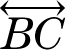 . The two-ended arrow over the letters tells you that the letters are describing a line. You can name a line by any two points that lie on the line. A plane is a third undefined term. A plane is a flat surface that extends infinitely in all directions.
. The two-ended arrow over the letters tells you that the letters are describing a line. You can name a line by any two points that lie on the line. A plane is a third undefined term. A plane is a flat surface that extends infinitely in all directions.