Table of Contents
Guide
Page List

Copyright 2021, 2016, 2011 by Kaplan, Inc., d/b/a Barrons Educational Series All rights reserved. No part of this publication may be reproduced or distributed in any form or by any means without the written permission of the copyright owner. Published by Kaplan, Inc., d/b/a Barrons Educational Series 750 Third Avenue New York, NY 10017
www.barronseduc.com ISBN: 978-1-5062-7318-1 10 9 8 7 6 5 4 3 2 1 All rights reserved under International and Pan-American Copyright Conventions. By payment of the required fees, you have been granted the non-exclusive, non-transferable right to access and read the text of this eBook on screen. No part of this text may be reproduced, transmitted, downloaded, decompiled, reverse engineered, or stored in or introduced into any information storage and retrieval system, in any form or by any means, whether electronic or mechanical, now known or hereinafter invented, without the express written permission of the publisher.
Contents
Painless pre-algebra? Impossible, you think.
Not really. Math iseasy or at least it can be with the help of this book! Whether you are learning pre-algebra for the first time, or you aretrying to remember what youve learned but have forgotten, thisbook is for you. It provides a clear introduction to pre-algebra that isboth fun and instructive. Dont be afraid. Dive inits painless! Painless Icons and Features This book is designed with several unique features to help makelearning pre-algebra easy.  PAINLESS TIP You will see Painless Tips throughout the book.
PAINLESS TIP You will see Painless Tips throughout the book.
These include helpful tips, hints, and strategies on the surrounding topics.  CAUTIONMajor Mistake Territory! Caution boxes will help you avoid common pitfalls or mistakes. Be sure to read them carefully.
CAUTIONMajor Mistake Territory! Caution boxes will help you avoid common pitfalls or mistakes. Be sure to read them carefully.  MATH TALK! These boxes translate "math talk" into plain English to make it even easier to understand math.
MATH TALK! These boxes translate "math talk" into plain English to make it even easier to understand math.  BRAIN TICKLERS There are brain ticklers throughout each chapter in the book. These quizzes are designed to make sure you understand what youve just learned and to test your progress as you move forward in the chapter.
BRAIN TICKLERS There are brain ticklers throughout each chapter in the book. These quizzes are designed to make sure you understand what youve just learned and to test your progress as you move forward in the chapter.
Complete all the Brain Ticklers and check your answers. If you get any wrong, make sure to go back and review the topics associated with the questions you missed. PAINLESS STEPS Complex procedures are divided into a series of painless steps. These steps help you solve problems in a systematic way. Follow the steps carefully, and youll be able to solve most pre-algebra problems. EXAMPLES Most topics include examples with solutions.
If you are having trouble, research shows that writing or copying the problem may help you understand it. ILLUSTRATIONS Painless Pre-Algebra is full of illustrations to help you better understand pre-algebra topics. Youll find graphs, charts, and more instructive illustrations to help you along the way. SIDEBARS These shaded boxes contain extra information that relates to the surrounding topics. Sidebars can include detailed examples or practice tips to help keep pre-algebra interesting and painless. Exponents are a shorthand way of writing repeated multiplication.
For example, 2 2 2 2 2 is read as 2 times 2 times 2 times 2 times 2. This multiplication problem can also be written in exponential form. 2 2 2 2 2 = 25 25 means the number 2 is a factor 5 times If a number is written in exponential form, the exponent tells how many times the base is used as a factor. 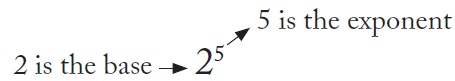
 MATH TALK! Here are a few ways to say and write exponential expressions:
MATH TALK! Here are a few ways to say and write exponential expressions:
| | a4 |
| 3 times 3 | 4 times 4 times 4 | a times a times a times a |
| Three to the | Four to the | a to the |
| second power | third power | fourth power |
| 3 squared | Four cubed |
To evaluate exponents, just remember that using exponents is just a short way of writing repeated multiplication. 32 = 3 3 = 933 = 3 3 3 = 2734 = 3 3 3 3 = 81

CAUTIONMajor Mistake Territory! 52 means 5 times 5, which equals 25. 52 does not mean 5 times 2, which equals ten. The exponent tells you how many times to multiply the base by itself.
We can also use exponents with negative numbers. (2)2 = (29) (2) = 4 (3)2 = (3) (3) = 9 (10)2 = (10) (10) = 100 When you square a negative number, the answer is always positive. (2)3 = (2) (2) (2) = 8 (3)3 = (3) (3) (3) = 27 (4)3 = (4) (4) (4) = 64 When you raise a negative number to the third power, or cube it, the answer is always negative.  PAINLESS TIP Rules for Exponents of Negative Numbers A negative number raised to an even power is always a positive number. A negative number raised to an odd power is always a negative number. (2)2 = (2) (2) = 4 (2)3 = (2) (2) (2) = 8 (2)4 = (2) (2) (2) (2) = 16 (2)5 = (2) (2) (2) (2) (2) = 32 (1)100 = 1
PAINLESS TIP Rules for Exponents of Negative Numbers A negative number raised to an even power is always a positive number. A negative number raised to an odd power is always a negative number. (2)2 = (2) (2) = 4 (2)3 = (2) (2) (2) = 8 (2)4 = (2) (2) (2) (2) = 16 (2)5 = (2) (2) (2) (2) (2) = 32 (1)100 = 1
(1)89 = 1 BRAIN BUSTER! When simplifying exponents, watch out for those pesky negative signs.
A common mistake is interpreting 32 as (3)2. 32 means the number 3 is squared and the answer is negative. The negative sign is like multiplying 32 by (1). It is the same as (1)(3)(3) = 9. vs. (3)2 means the number 3 is squared.
So (3) (3) = 9. Example 1: (2)3 = (2) (2) (2) = 8vs.23 = (1)(2)(2)(2) = 8 Here, the number (2) is cubed.Here, 2 is cubed, and then the answer is negative. Example 2: (3)4 = (3) (3) (3) (3) = 81vs.34 = (1)(3)(3)(3)(3) = 81 Another important exponent rule is the zero power rule. Any number raised to the zero power equals 1. Be careful what number is being raised to the zero power. 1.23 2.42 3.82 4.103 5.70 6.(3)3 7.(5)2 8.(20)0 9.42 10.(4)2 11.52 12.200 (Answers are on page .) PAINLESS TIP Multiplying Powers with the Same Base Exponents are a shorthand way of writing repeated multiplication. 1.23 2.42 3.82 4.103 5.70 6.(3)3 7.(5)2 8.(20)0 9.42 10.(4)2 11.52 12.200 (Answers are on page .)
PAINLESS TIP Multiplying Powers with the Same Base Exponents are a shorthand way of writing repeated multiplication. 1.23 2.42 3.82 4.103 5.70 6.(3)3 7.(5)2 8.(20)0 9.42 10.(4)2 11.52 12.200 (Answers are on page .)















 Copyright 2021, 2016, 2011 by Kaplan, Inc., d/b/a Barrons Educational Series All rights reserved. No part of this publication may be reproduced or distributed in any form or by any means without the written permission of the copyright owner. Published by Kaplan, Inc., d/b/a Barrons Educational Series 750 Third Avenue New York, NY 10017 www.barronseduc.com ISBN: 978-1-5062-7318-1 10 9 8 7 6 5 4 3 2 1 All rights reserved under International and Pan-American Copyright Conventions. By payment of the required fees, you have been granted the non-exclusive, non-transferable right to access and read the text of this eBook on screen. No part of this text may be reproduced, transmitted, downloaded, decompiled, reverse engineered, or stored in or introduced into any information storage and retrieval system, in any form or by any means, whether electronic or mechanical, now known or hereinafter invented, without the express written permission of the publisher.
Copyright 2021, 2016, 2011 by Kaplan, Inc., d/b/a Barrons Educational Series All rights reserved. No part of this publication may be reproduced or distributed in any form or by any means without the written permission of the copyright owner. Published by Kaplan, Inc., d/b/a Barrons Educational Series 750 Third Avenue New York, NY 10017 www.barronseduc.com ISBN: 978-1-5062-7318-1 10 9 8 7 6 5 4 3 2 1 All rights reserved under International and Pan-American Copyright Conventions. By payment of the required fees, you have been granted the non-exclusive, non-transferable right to access and read the text of this eBook on screen. No part of this text may be reproduced, transmitted, downloaded, decompiled, reverse engineered, or stored in or introduced into any information storage and retrieval system, in any form or by any means, whether electronic or mechanical, now known or hereinafter invented, without the express written permission of the publisher.  PAINLESS TIP You will see Painless Tips throughout the book.
PAINLESS TIP You will see Painless Tips throughout the book. CAUTIONMajor Mistake Territory! Caution boxes will help you avoid common pitfalls or mistakes. Be sure to read them carefully.
CAUTIONMajor Mistake Territory! Caution boxes will help you avoid common pitfalls or mistakes. Be sure to read them carefully.  MATH TALK! These boxes translate "math talk" into plain English to make it even easier to understand math.
MATH TALK! These boxes translate "math talk" into plain English to make it even easier to understand math.  BRAIN TICKLERS There are brain ticklers throughout each chapter in the book. These quizzes are designed to make sure you understand what youve just learned and to test your progress as you move forward in the chapter.
BRAIN TICKLERS There are brain ticklers throughout each chapter in the book. These quizzes are designed to make sure you understand what youve just learned and to test your progress as you move forward in the chapter.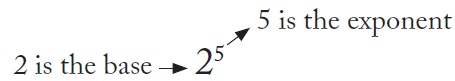
 PAINLESS TIP Rules for Exponents of Negative Numbers A negative number raised to an even power is always a positive number. A negative number raised to an odd power is always a negative number. (2)2 = (2) (2) = 4 (2)3 = (2) (2) (2) = 8 (2)4 = (2) (2) (2) (2) = 16 (2)5 = (2) (2) (2) (2) (2) = 32 (1)100 = 1
PAINLESS TIP Rules for Exponents of Negative Numbers A negative number raised to an even power is always a positive number. A negative number raised to an odd power is always a negative number. (2)2 = (2) (2) = 4 (2)3 = (2) (2) (2) = 8 (2)4 = (2) (2) (2) (2) = 16 (2)5 = (2) (2) (2) (2) (2) = 32 (1)100 = 1