Numerical
Methods
in Engineering
and Science
LICENSE, DISCLAIMER OF LIABILITY, AND LIMITED WARRANTY By purchasing or using this book (the Work), you agree that this license grants permission to use the contents contained herein, but does not give you the right of ownership to any of the textual content in the book or ownership to any of the information or products contained in it. This license does not permit uploading of the Work onto the Internet or on a network (of any kind) without the written consent ofthe Publisher. Duplication or dissemination of any text, code, simulations, images, etc. contained herein is limited to and subject to licensing terms for the respective products, and permission must be obtained from the Publisher or the owner of the content, etc., in order to reproduce or network any portion of the textual material (in any media) that is contained in the Work. M ERCURY L EARNING AND I NFORMATION (MLI or the Publisher) and anyone involved in the creation, writing, or production of the companion disc, accompanying algorithms, code, or computer programs (the software), and any accompanying Web site or software of the Work, cannot and do not warrant the performance or results that might be obtained by using the contents of the Work. The author, developers, and the Publisher have used their best efforts to insure the accuracy and functionality of the textual material and/or programs contained in this package; we, however, make no warranty of any kind, express or implied, regarding the performance of these contents or programs. The Work is sold as is without warranty (except for defective materials used in manufacturing the book or due to faulty workmanship). The author, developers, and the publisher of any accompanying content, and anyone involved in the composition, production, and manufacturing of this work will not be liable for damages of any kind arising out of the use of (or the inability to use) the algorithms, source code, computer programs, or textual material contained in this publication. This includes, but is not limited to, loss of revenue or profit, or other incidental, physical, or consequential damages arising out of the use of this Work. The sole remedy in the event of a claim of any kind is expressly limited to replacement of the book, and only at the discretion of the Publisher. The use of implied warranty and certain exclusions vary from state to state, and might not apply to the purchaser of this product. Numerical
Methods
in Engineering
and Science C, C++, and MATLAB B. S. Grewal Copyright 2019 by Mercury Learning and Information LLC . All rights reserved. Copyright 2019 by Mercury Learning and Information LLC . All rights reserved.
Original Title and Copyright: Numerical Methods in Engineering and Science 3/E.
2014 by Khanna Publishers. This publication, portions of it, or any accompanying software may not be reproduced in any way, stored in a retrieval system of any type, or transmitted by any means, media, electronic display or mechanical display, including, but not limited to, photocopy, recording, Internet postings, or scanning, without prior permission in writing from the publisher. Publisher: David Pallai
M ERCURY L EARNING AND I NFORMATION
22841 Quicksilver Drive
Dulles, VA 20166
info@merclearning.com
www.merclearning.com
(800) 232-0223 B. S. Grewal. Numerical Methods in Engineering and Science: C, C++, and MATLAB.
ISBN: 978-1-68392-128-8 The publisher recognizes and respects all marks used by companies, manufacturers, and developers as a means to distinguish their products. All brand names and product names mentioned in this book are trademarks or service marks of their respective companies. Any omission or misuse (of any kind) of service marks or trademarks, etc. is not an attempt to infringe on the property of others. Library of Congress Control Number: 2018935002 181920321 This book is printed on acid-free paper in the United States of America. Our titles are available for adoption, license, or bulk purchase by institutions, corporations, etc.
For additional information, please contact the Customer Service Dept. at 800-232-0223(toll free). All of our titles are available in digital format at authorcloudware.com and other digital vendors. The sole obligation of M ERCURY L EARNING AND I NFORMATION to the purchaser is to replace the book, based on defective materials or faulty workmanship, but not based on the operation or functionality of the product. In This Chapter - Introduction
- Accuracy of numbers
- Errors
- Useful rules for estimating errors
- Error propagation
- Error in the approximation of a function
- Error in a series approximation
- Order of approximation
- Growth of error
- Objective type of questions
The limitations of analytical methods in practical applications have led scientists and engineers to evolve numerical methods. We know that exact methods often fail in drawing plausible inferences from a given set of tabulated data or in finding roots of transcendental equations or in solving non-linear differential equations. There are many more such situations where analytical methods are unable to produce desirable results. The aim of numerical analysis is therefore, to provide constructive methods for obtaining answers to such problems in a numerical form. With the advent of high speed computers and increasing demand for numerical solution to various problems, numerical techniques have become indispensible tools in the hands of engineers and scientists. The aim of numerical analysis is therefore, to provide constructive methods for obtaining answers to such problems in a numerical form. With the advent of high speed computers and increasing demand for numerical solution to various problems, numerical techniques have become indispensible tools in the hands of engineers and scientists. The input information is rarely exact since it comes from some measurement or the other and the method also introduces further error. As such, the error in the final result may be due to an error in the initial data or in the method or both. Our effort will be to minimize these errors, so as to get the best possible results. We therefore begin by explaining various kinds of approximations and errors which may occur in a problem and derive some results on error propagation in numerical calculations. - Approximate numbers. There are two types of numbers: exact and approximate. etc. etc.
But there are numbers such as 4/3 ( = 1.33333...), 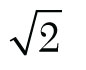 (= 1.414213...) and ( = 3.141592...) which cannot be expressed by a finite number of digits. These may be approximated by numbers 1.3333, 1.4142 and 3.1416, respectively. Such numbers which represent the given numbers to a certain degree of accuracy are called approximate numbers. (= 1.414213...) and ( = 3.141592...) which cannot be expressed by a finite number of digits. These may be approximated by numbers 1.3333, 1.4142 and 3.1416, respectively. Such numbers which represent the given numbers to a certain degree of accuracy are called approximate numbers. - Significant figures. The digits used to express a number are called significant digits (figures). Thus each of the numbers 7845, 3.589, and 0.4758 contains four significant figures while the numbers 0.00386, 0.000587, and 0.0000296 contain only three significant figures since zeros only help to fix the position of the decimal point. Similarly the numbers 45000 and 7300.00 have two significant figures only.
- Rounding off. There are numbers with large number of digits, e.g., 22/7 = 3.142857143. In practice, it is desirable to limit such numbers to a manageable number of digits such as 3.14 or 3.143.
|











 Copyright 2019 by Mercury Learning and Information LLC . All rights reserved.
Copyright 2019 by Mercury Learning and Information LLC . All rights reserved.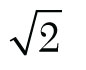 (= 1.414213...) and ( = 3.141592...) which cannot be expressed by a finite number of digits. These may be approximated by numbers 1.3333, 1.4142 and 3.1416, respectively. Such numbers which represent the given numbers to a certain degree of accuracy are called approximate numbers.
(= 1.414213...) and ( = 3.141592...) which cannot be expressed by a finite number of digits. These may be approximated by numbers 1.3333, 1.4142 and 3.1416, respectively. Such numbers which represent the given numbers to a certain degree of accuracy are called approximate numbers.