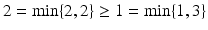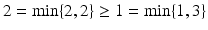1. Introduction
The best introduction to game theory is by way of examples. This chapter starts with a global definition in Sect. briefly comments on the distinction between cooperative and noncooperative game theory.
1.1 A Definition
Game theory studies situations of competition and cooperation between several involved parties by using mathematical methods. This is a broad definition but it is consistent with the large number of applications. These applications range from strategic questions in warfare to understanding economic competition, from economic or social problems of fair distribution to behavior of animals in competitive situations, from parlor games to political voting systemsand this list is certainly not exhaustive.
Game theory is an official mathematical discipline (American Mathematical Society Classification code 91A) but it is developed and applied mostly by economists. In economics, articles and books on game theory and applications are found in particular under the Journal of Economic Literature codes C7x. The list of references at the end of this book contains many textbooks and other books on game theory.
1.2 Some History
In terms of applications, game theory is a broad discipline, and it is therefore not surprising that game-theoretic situations can be recognized in the Bible (Brams, ).
One of the first formal works on game theory is Zermelo () for a comprehensive study of the history of game theory up to 1945.
The title of the book of von Neumann and Morgenstern reveals the intention of the authors that game theory was to be applied to economics. Nevertheless, in the 1950s and 1960s the further development of game theory was mainly the domain of mathematicians. Seminal articles in this period were the papers by Nash): many examples still used in game theory can be traced back to this source, like the Prisoners Dilemma and the Battle of the Sexes.
In the late 1960s and 1970s of the previous century game theory became accepted as a new formal language for economics in particular. This development was stimulated by the work of Harsanyi () on (sub)game perfect Nash equilibrium.
In 1994, Nash, Harsanyi and Selten jointly received the Nobel prize in economics for their work in game theory. Since then, many Nobel prizes in economics have been awarded for achievements in game theory or closely related to game theory: Mirrlees and Vickrey (in 1996), Sen (in 1998), Akerlof, Spence and Stiglitz (in 2001), Aumann and Schelling (in 2005), Hurwicz, Maskin and Myerson (in 2007), and Roth and Shapley (in 2012).
From the 1980s on, large parts of economics have been rewritten and further developed using the ideas, concepts and formal language of game theory. Articles on game theory and applications can be found in many economic journals. Journals explicitly focusing on game theory include the International Journal of Game Theory , Games and Economic Behavior , and International Game Theory Review . Game theorists are organized within the Game Theory Society , see http://www.gametheorysociety.org/ .
1.3 Examples
Every example in this section is based on a story . Each time this story is presented first and, next, it is translated into a formal mathematical model . Such a mathematical model is an alternative description, capturing the essential ingredients of the story with the omission of details that are considered unimportant: the mathematical model is an abstraction of the story. After having established the model, we spend some lines on how to solve it: we say something about how the players should or would act. In more philosophical terms, these solutions can be normative or positive in nature, or somewhere in between, but often such considerations are left as food for thought for the reader. As a general remark, a basic distinction between optimization theory and game theory is that in optimization it is usually clear when some action or choice is optimal, whereas in game theory we deal with human (or, more generally, animal) behavior and then it may be less clear when an action is optimal or even what optimality means.
Each example is concluded by further comments , possibly including a short preview on the treatment of the exemplified game in the book. The examples are grouped in subsections on zero-sum games, nonzero-sum games, extensive form games, cooperative games, and bargaining games.
1.3.1 Zero-Sum Games
The first example is based on a military situation staged in World War II.
1.3.1.1 The Battle of the Bismarck Sea
Story The game is set in the South-Pacific in 1943. The Japanese admiral Imamura has to transport troops across the Bismarck Sea to New Guinea, and the American admiral Kenney wants to bomb the transport. Imamura has two possible choices: a short Northern route (2 days) or a long Southern route (3 days), and Kenney must choose one of these routes to send his planes to. If he chooses the wrong route he can call back the planes and send them to the other route, but the number of bombing days is reduced by 1. We assume that the number of bombing days represents the payoff to Kenney in a positive sense and to Imamura in a negative sense.
Model The Battle of the Bismarck Sea problem can be modelled using the following table:
This table represents a game with two players, namely Kenney and Imamura. Each player has two possible choices; Kenney (player 1) chooses a row, Imamura (player 2) chooses a column, and these choices are to be made independently and simultaneously. The numbers represent the payoffs to Kenney. For instance, the number 2 up left means that if Kenney and Imamura both choose North, the payoff to Kenney is 2 and the payoff to Imamura is 2. Thus, the convention is to let the numbers denote the payments from player 2 (the column player) to player 1 (the row player). This game is an example of a zero-sum game because the sum of the payoffs is always equal to zero.
Solution In this particular example, it does not seem difficult to predict what will happen. By choosing North, Imamura is always at least as well off as by choosing South, as is easily inferred from the above table of payoffs. So it is safe to assume that Imamura chooses North, and Kenney, being able to perform this same kind of reasoning, will then also choose North, since that is the best reply to the choice of North by Imamura. Observe that this game is easy to analyze because one of the players (Imamura) has a dominated choice, namely South: no matter what the opponent (Kenney) decides to do, North is at least as good as South, and sometimes better.
Another way to look at this game is to observe that the payoff 2 resulting from the combination (North, North) is maximal in its column (21) and minimal in its row (22). Such a position in the matrix is called a saddlepoint . In such a saddlepoint, neither player has an incentive to deviate unilaterally. (As will become clear later, this implies that the combination (North, North) is a Nash equilibrium .) Also observe that, in such a saddlepoint, the row player maximizes his minimal payoff (because