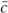Shu Hotta - Mathematical Physical Chemistry: Practical and Intuitive Methodology

This Springer imprint is published by the registered company Springer Nature Singapore Pte Ltd.

The registered company address is: 152 Beach Road, #21-01/04 Gateway East, Singapore 189721, Singapore

This book is the second edition ofMathematical Physical Chemistry. Mathematics is a common language of natural science including physics, chemistry, and biology. Although the words mathematical physics and physical chemistry (or chemical physics) are commonly used, mathematical physical chemistry sounds rather uncommon. Therefore, it might well be reworded as the mathematical physics for chemists. The book title could have been, for instance, The Mathematics of Physics and Chemistry accordingly, in tribute to the famous book that was written three-quarters of a century ago by H. Margenau and G. M. Murphy. Yet, the word mathematical physical chemistry is expected to be granted citizenship, considering that chemistry and related interdisciplinary fields such as materials science and molecular science are becoming increasingly mathematical.

The main concept and main theme remain unchanged, but this books second edition contains the theory of analytic functions and the theory of continuous groups. Both the theories are counted as one of the most elegant theories of mathematics. The mathematics of these topics is of a somewhat advanced level and something like a sufficient condition for chemists, whereas that of the first edition may be a prerequisite (or a necessary condition) for them. Therefore, chemists (or may be physicists as well) can creatively use the two editions. In association with these major additions to the second edition, the author has disposed the mathematical topics (the theory of analytic functions, Greens functions, exponential functions of matrices, and the theory of continuous groups) at the last chapter of individual parts (Part I through Part IV).

At the same time, the author has also made several specific revisions including the introductory discussion on the perturbation method and variational method, both of which can be effectively used for gaining approximate solutions of various quantum-mechanical problems. As another topic, the author has presented the recent progress on organic lasers. This topic is expected to help develop high-performance light-emitting devices, one of the important fields of materials science. As in the case of the first edition, readers benefit from going freely back and forth across the whole topics of this book.

Once again, the author wishes to thank many students for valuable discussions and Dr. Shinichi Koizumi at Springer for giving him an opportunity to write this book.

The contents of this book are based upon manuscripts prepared for both undergraduate courses of Kyoto Institute of Technology by the author entitled Polymer Nanomaterials Engineering and Photonics Physical Chemistry and a masters course lecture of Kyoto Institute of Technology by the author entitled Solid-State Polymers Engineering.

This book is intended for graduate and undergraduate students, especially those who major in chemistry and, at the same time, wish to study mathematical physics. Readers are supposed to have a basic knowledge of analysis and linear algebra. However, they are not supposed to be familiar with the theory of analytic functions (i.e., complex analysis), even though it is desirable to have relevant knowledge about it.

At the beginning, mathematical physics looks daunting to chemists, as used to be the case with myself as a chemist. The book introduces the basic concepts of mathematical physics to chemists. Unlike other books related to mathematical physics, this book makes a reasonable selection of material so that students majoring in chemistry can readily understand the contents in spontaneity. In particular, we stress the importance of practical and intuitive methodology. We also expect engineers and physicists to benefit from reading this book.

In Part I and Part II, the book describes quantum mechanics and electromagnetism. Relevance between the two is well considered. Although quantum mechanics covers the broad field of modern physics, in Part I we focus on a harmonic oscillator and a hydrogen (like) atom. This is because we can study and deal with many of fundamental concepts of quantum mechanics within these restricted topics. Moreover, knowledge acquired from the study of the topics can readily be extended to practical investigation of, e.g., electronic states and vibration (or vibronic) states of molecular systems. We describe these topics by both analytic method (that uses differential equations) and operator approach (using matrix calculations). We believe that the basic concepts of quantum mechanics can be best understood by contrasting the analytical and algebraic approaches. For this reason, we give matrix representations of physical quantities whenever possible. Examples include energy eigenvalues of a quantum-mechanical harmonic oscillator and angular momenta of a hydrogen-like atom. At the same time, these two physical systems supply us with a good opportunity to study classical polynomials, e.g., Hermite polynomials, (associated) Legendre polynomials, Laguerre polynomials, Gegenbauer polynomials, and special functions, more generally. These topics constitute one of the important branches of mathematical physics. One of the basic concepts of quantum mechanics is that a physical quantity is represented by a Hermitian operator or matrix. In this respect, the algebraic approach gives a good opportunity to get familiar with this concept. We present tangible examples for this. We also emphasize the importance of the notion of Hermiticity of a differential operator. We often encounter a unitary operator or unitary transformation alongside the notion of Hermitian operators. We show several examples of unitary operators in connection with transformation of vectors and coordinates.