1. Introduction
The planetary boundary layer (PBL) is the bottom layer of the troposphere, i.e. that part in contact with the underlying land or ocean surface. Not only is the PBL the atmospheres part which humans are primarily exposed to, but also does it govern the exchange of energy, momentum and humidity between the solid earth and the free atmosphere, the tropospheres part located immediately above the PBL. While the upper end of the PBL can be defined in numerous ways (on the earth, it ranges between some tens of meters and few kilometers), its lower limit is the surface itself. There, velocity and temperature of air need to match that of the underlying mediumbe it an immovable wall, water or floating ice. At the upper end, the velocity is set by the wind and temperature in the free atmosphere inducing gradients in both the velocity and temperature across the PBL. Due to the huge vertical extent of the boundary layer and the low viscosity of air, even small vertical variations in the velocity deem the flow of air in the PBL turbulent which intensifies the vertical exchange of momentum, mass and energy by orders of magnitude.
Vertical gradients in temperature are mostly a consequence of differential heating or radiative processes, and in the absence of humidity and advection, they are caused by heating or cooling at the surface. Temperature and density variations are linked through the equation of state for air as an ideal gas. Depending on their sign, density variations may enhance or damp turbulence in the PBL, whose characteristics crucially depend on its density stratification. When the surface is relatively cooler than the air in the free atmosphere, density perturbations are damped: the density stratification is stable. The PBL under the impact of stable density stratification (SBL) is the object of research in this work, where fundamental aspects of wall-bounded stably-stratified turbulence are addressed, and their implications for the SBL are laid out.
If the surface cools sufficiently, turbulence is not only damped, but sometimes observed to cease partially or even entirely (Schlichting ). This work embarks on a new tool in the context of the SBL, namely the direct numerical simulation (DNS) of turbulent flow, to re-establish an old perspectivethat of fundamental fluid mechanics. Links between the extensive bodies of work devoted to stably stratified fluids and the SBL are established and exploited to gain new insight into the dynamics of the SBL.
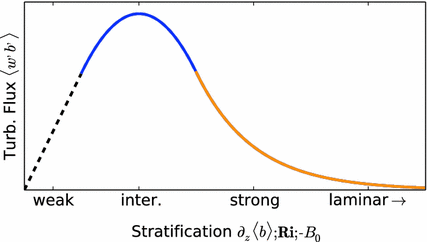
Fig. 1.1
Idealized schematic of the turbulent heat flux in the surface layer under increasing static stability; here, the turbulent heat flux is presented as a boundary-condition problem
1.1 Turbulence Regimes
Often, SBLs are classified into three regimes (Mahrt et al. ). First, in the weakly stable regime (black dashed line), temperature behaves almost as a passive scalar, and the PBLs structure is indistinguishable from the neutral reference: weakness of the temperature gradients limits the turbulent heat exchange. Consequently, if stratification is strengthened slightly, the turbulent heat flux increases monotonically as a function of the stratification. Second, in the intermediately stable regime (blue line), the turbulent heat flux stagnates if stratification is strengthened; an increased temperature gradient is compensated by a decrease of vertical velocity fluctuations. Third, in the very stable regime (orange line), stratification drastically alters the SBLs turbulence structure to the degree that the weakness of turbulent motion limits the vertical heat exchange: The turbulent heat flux decreases with strengthening stratification. If strong enough, stratification canlocally or globallylead to the absence of turbulence.
Although the very stable regime can be commonly observed in the atmosphere (Mahrt et al. ).
1.2 Global Intermittency
A well-accepted hypothesis is that the cessation of turbulence is not an onoff process but rather a complex transition beginning with global intermittency, the localized absence of turbulence in an otherwise turbulent boundary layer. There exists a well-developed conceptual framework to ascertain whether a laminar flow exposed to a density stratification becomes turbulent: TaylorGoldstein stability analysis and the MilesHoward theorem (Di Prima and Swinney ).
The coexistence of locally laminar and locally turbulent flow in a single configuration is already mentioned by Corrsin () postulates that regions of fully developed turbulence exist for a sufficiently long period of time to allow for the establishment of local isotropy inside them. When the non-turbulent fraction of the turbulent flow is taken into account, his experimental data agree better with the prediction of K41.
Using an advanced method to determine the intermittency factor in a boundary layer (based on high-frequency velocity oscillations; cf. Townsend () introduces conditional sampling and averaging techniques to study separately the turbulent and non-turbulent flow regions in the intermittent part of a boundary layer.
The aforementioned studies are concerned with the case where non-turbulent flow exists aloft or around some region of turbulent motion. Another variant occurs when stabilizing body forces act on a flow and cause the decay, cessation or absence of turbulence. In stratified channels, re-laminarization was shown not to occur as an onoff process in time but rather as a complex transition from a turbulent to a non-turbulent state (Armenio and Sarkar ).
To the authors knowledge, occurrence of global intermittency in atmospheric configurations has not yet reflected into an application of the conditioning methods described above to study separately the turbulent and non-turbulent sub-volumes in a rotating and stratified boundary layer. The challenge is twofold: First, small-scale derivatives have to be measured with sufficient accuracy to determine a vorticity-based intermittency factor
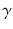
(Kuznetsov et al. ). Regarding numerical simulations, sufficiently resolved data in space and time are made available as part of this work and global intermittency is quantified here using direct numerical simulations of Ekman flow. The second challenge is related to the occurrence of global intermittency close to the wall. While a vorticity-based partitioning of the flow detects external intermittency in the outer layer of neutrally stratified flows, there are problems with global intermittency close to wall. There, large gradients in non-turbulent regions may falsely indicate the existence of turbulence. To overcome this second challenge, this work proposes an analysis of the flow combining the intermittency factor with a high-pass filter operation.
A different problem is the origin of global intermittency. It has been shown from observations globally intermittent turbulence can be triggered by a variety of external disturbances including orographic obstacles (Acevedo and Fitzjarrald ) have led to qualitative models of turbulence collapse and global intermittency. Global intermittency was, however, not investigated, and it remains unclear whether global intermittency can occur in a SBL without these external triggering mechanisms. In this work, evidence is provided that global intermittency is a process intrinsic to the SBL and does not necessarily rely on these triggering mechanisms as a precursor.













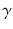 (Kuznetsov et al. ). Regarding numerical simulations, sufficiently resolved data in space and time are made available as part of this work and global intermittency is quantified here using direct numerical simulations of Ekman flow. The second challenge is related to the occurrence of global intermittency close to the wall. While a vorticity-based partitioning of the flow detects external intermittency in the outer layer of neutrally stratified flows, there are problems with global intermittency close to wall. There, large gradients in non-turbulent regions may falsely indicate the existence of turbulence. To overcome this second challenge, this work proposes an analysis of the flow combining the intermittency factor with a high-pass filter operation.
(Kuznetsov et al. ). Regarding numerical simulations, sufficiently resolved data in space and time are made available as part of this work and global intermittency is quantified here using direct numerical simulations of Ekman flow. The second challenge is related to the occurrence of global intermittency close to the wall. While a vorticity-based partitioning of the flow detects external intermittency in the outer layer of neutrally stratified flows, there are problems with global intermittency close to wall. There, large gradients in non-turbulent regions may falsely indicate the existence of turbulence. To overcome this second challenge, this work proposes an analysis of the flow combining the intermittency factor with a high-pass filter operation.