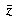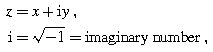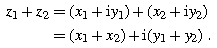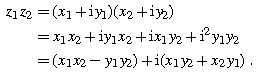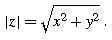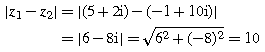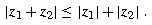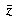Part 1
Fundamentals of Mechanical Engineering
Karl-Heinrich Grote and Erik K. Antonsson (eds.) Springer Handbook of Mechanical Engineering 10.1007/978-3-540-30738-9_1 Springer-Verlag 2009
1. Introduction to Mathematics for Mechanical Engineering
Ramin S. Esfandiari 1
(1)
Department of Mechanical & Aerospace Engineering, California State University, 90840 Long Beach, CA, USA
Ramin S. Esfandiari
Email:
URL: http://www.csulb.edu/colleges/coe/mae/index.shtml
1.1
1.1.1
1.1.1.1
1.1.1.2
1.1.1.3
1.1.1.4
1.1.1.5
1.1.2
1.1.2.1
1.2
1.2.1
1.2.1.1
1.2.1.2
1.2.1.3
1.2.1.4
1.2.2
1.2.3
1.2.3.1
1.2.3.2
1.2.3.3
1.2.3.4
1.2.3.5
1.2.3.6
1.3
1.3.1
1.3.1.1
1.3.1.2
1.3.1.3
1.3.1.4
1.3.2
1.3.2.1
1.3.3
1.3.3.1
1.3.3.2
1.3.4
1.3.4.1
1.3.4.2
1.3.5
1.4
1.4.1
1.4.1.1
1.4.2
1.5
1.5.1
1.5.1.1
1.5.1.2
1.5.1.3
1.5.1.4
1.5.1.5
1.5.2
1.5.2.1
1.5.2.2
1.5.2.3
1.5.2.4
1.5.3
1.5.3.1
1.5.3.2
Abstract
This chapter is concerned with fundamental mathematical concepts and methods pertaining to mechanical engineering. The topics covered include complex analysis, differential equations, Laplace transformation, Fourier analysis, and linear algebra. These basic concepts essentially act as tools that facilitate the understanding of various ideas, and implementation of many techniques, involved in different branches of mechanical engineering. Complex analysis, which refers to the study of complex numbers, variables and functions, plays an important role in a wide range of areas from frequency response to potential theory. The significance of ordinary differential equations (ODEs) is observed in situations involving the rate of change of a quantity with respect to another. A particular area that requires a thorough knowledge of ODEs is the modeling, analysis, and control of dynamic systems. Partial differential equations (PDEs) arise when dealing with quantities that are functions of two or more variables; for instance, equations of motions of beams and plates. Higher-order differential equations are generally difficult to solve. To that end, the Laplace transformation is used to transform the data from the time domain to the so-called s -domain, where equations are algebraic and hence easy to treat. The solution of the differential equation is ultimately obtained when information is transformed back to time domain. Fourier analysis is comprised of Fourier series and Fourier transformation. Fourier series are a specific trigonometric series representation of a periodic signal, and frequently arise in areas such as system response analysis. Fourier transformation maps information from the time to the frequency domain, and its extension leads to the Laplace transformation. Linear algebra refers to the study of vectors and matrices, and plays a central role in the analysis of systems with large numbers of degrees of freedom.
Abbreviations
BVP
boundary-value problem
IVP
initial-value problem
ODE
ordinary differential equation
PDE
partial differential equations
1.1 Complex Analysis
Complex numbers, variables and functions are the main focus of this section. We will begin with complex numbers, their representations, as well as properties. The idea is then extended to complex variables and their functions.
1.1.1 Complex Numbers
A complex number z appears in the rectangular form
where x and y are real numbers, called the real and imaginary parts of z , respectively, and denoted by x =Re( z ), y =Im( z ). For example, if z =1+2i, then x =Re( z )=1 and y =Im( z )=2. A complex number with zero real part is known as pure imaginary, e.g., z =4i. Two complex numbers are said to be equal if and only if their respective real and imaginary parts are equal. Addition of complex numbers is performed component-wise, that is, if z 1= x 1+i y 1 and z 2= x 2+i y 2, then
Multiplication of two complex numbers is performed in the same way as two binomials with the provision that i2=1, i3=i, i4=1, etc. need be taken into account, that is,
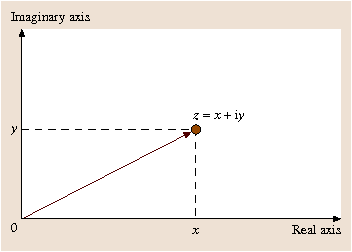
1.1.1.1 Complex Plane
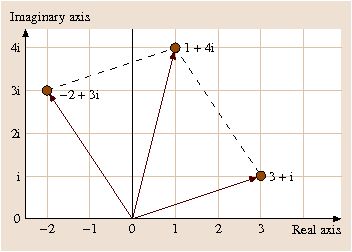
Since complex numbers consist of a real part and an imaginary part, they have a two-dimensional character, and hence may be represented geometrically as points in a Cartesian coordinate system, known as the complex plane. The x -axis of the complex plane is the real axis, and its y -axis is called the imaginary axis, (Fig.. It is then evident that their sum, z 1+ z 2=1+4i, is exactly what we would obtain by adding the corresponding position vectors of z 1 and z 2.
Fig. 1.1
Geometrical representation of complex numbers the complex plane
Fig. 1.2
Addition of complex numbers by vector addition
The magnitude of a complex number z = x +i y is defined as
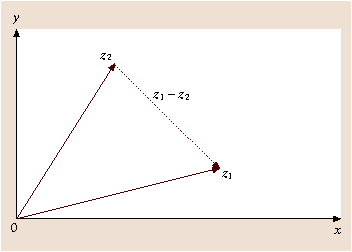
Geometrically, | z | is the distance from z to the origin of the complex plane. If z is real, it must be located on the x -axis, and its magnitude is equal to its absolute value. If z is pure imaginary ( z =i y ), then it is on the y -axis, and | z |=| y |. The quantity | z 1 z 2| gives the distance between z 1 and z 2 (Fig. ).
Fig. 1.3
Distance between two complex numbers
Example 1.1:
Distance
Given z 1=5+2i and z 2=1+10i, then
Addition of complex numbers obeys the triangle inequality,
Given a complex number z = x +i y , its conjugate, denoted by