1.1 The Meeting
The 1980s were an active decade for basic advances in sequence comparison algorithms. Michael Waterman, Temple Smith, Esko Ukkonen, Webb Miller, Gad Landau, David Lipman, Bill Pearson, and myself, among others, were all very active in this period of time and were working out the basic algorithms for comparing sequences, approximate pattern matching, and database searching (e.g. [].
In 1988, Webb Miller and I organized a small bioinformatics meeting in Bethesda, Maryland that included such notable figures as David Sankoff, Michael Waterman, Temple Smith, Eric Lander, Zvi Galil, Esko Ukkonen, David Lipman and other great investigators of that time. At the meeting Zvi Galil gave a talk about suffix trees [] and raised two questions that ultimately were answered:
Can suffix trees be built in a way that is independent of alphabet size s ?
Can a precomputed index such as a suffix tree of a large text be used to speed up searches for approximate matches to a string?
To understand the first question, one must recall that one can either use an s -element array in each suffix tree node to permit a search for a string of length p in a text of length n in O ( p ) time but requiring O ( ns ) space for the suffix tree, or one can use only O ( n ) space by using binary trees to decide which edge to follow out of a node, but resulting in O ( p log s ) time for the search. This question ultimately led Udi Manber and I to develop suffix arrays in late 1990 [], to be computed in O ( n ) time.
1.2 Filters and Neighborhoods
But it was the second question on the use of an index, such as a suffix tree, to speed searches for approximate matches that captured my attention immediately after the meeting. Most algorithmicists work on deterministic search algorithms meaning that the method finds exactly the set of locations in the text where a query approximately matches within some specified threshold, whereas a heuristic is an algorithm that finds most of the matches sought, but may miss a few, called a false negative , and may further report a few locations where a match doesnt actually occur, called a false positive . In between these two types of algorithms, a filter is an algorithm that has no false negatives but may produce false positives. That is, it produces a superset of the instances sought, or equivalently it filters out most of the locations where matches do not occur. A filter can be the first step of a deterministic algorithm simply by running a deterministic checking algorithm on the subset of locations reported by the filter. If the filter is much more efficient than the deterministic checker, then one ends up with a much more efficient search.
At the time, there were surprisingly no published methods using the simple idea of finding exact matches to k -mers (strings of length k ) from the query string [] even though this was fairly obvious and had been used in the heuristic method of FASTA. Shortly after the Bethesda meeting, I had the first and most important idea of looking for exact matches to strings in the neighborhood of k -mers selected from the query string. Let be a sequence comparison measure that given two strings v and w returns a numeric measure ( v , w ) of the degree to which they differ (e.g. the generalized Levenshtein metric). Given a string w the -neighborhood of w with respect to ,
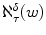
is the set of all strings v whose best alignment with w under scoring scheme is less than , i.e. { v :( v , w )}.
For this paper, except where mentioned otherwise, we are focusing on the approximate match problem where is the simple Levenshtein metric, which is the minimum number of insertions, deletions, and substitutions possible in an alignment between the two strings in question. That is, we seek matches of a query of length p to a text of length n , where up to e differences are allowed. Another way to phrase this, which we will use interchangeably, is that we seek -matches where = e / p is the length relative fraction of differences allowed. To illustrate the idea of a neighborhood under this metric, the 1-neighborhood of abba (or 25 %-neighborhood) is 1( abba )={ aaba , aabba , abaa , aba , abaa , ababa , abba , abbaa , abbab , abb , abbb , abbba , babba , bba , bbba }.
For the example above, notice that wherever one finds abaa one will also finds aba as it is a prefix of the former. So to find all matches to neighborhood strings it suffices to look up in an index only those that are not an extension of a shorter string in the same neighborhood. Let the condensed -neighborhood of w be the subset of these strings, i.e.
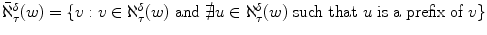
. For our example, the condensed 1-neighborhood of abba is
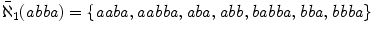
, a considerably smaller set of strings.
To illustrate the advantage of using (condensed) neighborhoods, consider looking for a match with nine differences to a query of length say 100. If one partitions the query into 10 strings of length 10, then by the Pigeon Hole principle, one of the 10 strings must exactly match in the database. So one can filter the text by looking for one of these 10 strings of length 10. But if one partitions the query into 5 strings of length 20, then by the Pigeon Hole principle, a string in the 1-neighborhoods of the five query parts must exactly match in the database. A rough estimate for the number of strings in the condensed e -neighborhood of a string of length k is
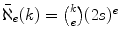
. Thus in our example we can filter the text by looking for one of 800 strings of length 20. Which filter is better? The probability of a random false positive for the k -mer filter is 10/ s 10 and for the neighborhood filter it is 800/ s 20. Thus the later filter produces s 10/80 fewer false positives. If s is 4 (e.g. the DNA alphabet) and n is 3109 (e.g. the size of the human genome) then the neighborhood filter produces 13,000 times fewer false positives, and reports in expectation 2.18 false positive, whereas the k -mer filter reports over 28,600!








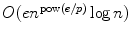 expected-time algorithm for finding all e -matches to a string of length p in a text of length n was completed in 1991. The function
expected-time algorithm for finding all e -matches to a string of length p in a text of length n was completed in 1991. The function 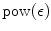 is 0 for =0 and concave increasing, so the algorithm is truly sublinear in that its running time is O ( n c ) for c <1 for sufficiently small. This paper reviews the history and the unfolding of the basic concepts, and it attempts to intuitively describe the deeper result whose time complexity, to this authors knowledge, has yet to be improved upon.
is 0 for =0 and concave increasing, so the algorithm is truly sublinear in that its running time is O ( n c ) for c <1 for sufficiently small. This paper reviews the history and the unfolding of the basic concepts, and it attempts to intuitively describe the deeper result whose time complexity, to this authors knowledge, has yet to be improved upon.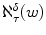 is the set of all strings v whose best alignment with w under scoring scheme is less than , i.e. { v :( v , w )}.
is the set of all strings v whose best alignment with w under scoring scheme is less than , i.e. { v :( v , w )}.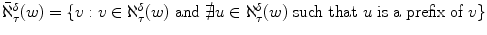 . For our example, the condensed 1-neighborhood of abba is
. For our example, the condensed 1-neighborhood of abba is 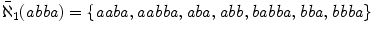 , a considerably smaller set of strings.
, a considerably smaller set of strings.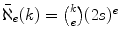 . Thus in our example we can filter the text by looking for one of 800 strings of length 20. Which filter is better? The probability of a random false positive for the k -mer filter is 10/ s 10 and for the neighborhood filter it is 800/ s 20. Thus the later filter produces s 10/80 fewer false positives. If s is 4 (e.g. the DNA alphabet) and n is 3109 (e.g. the size of the human genome) then the neighborhood filter produces 13,000 times fewer false positives, and reports in expectation 2.18 false positive, whereas the k -mer filter reports over 28,600!
. Thus in our example we can filter the text by looking for one of 800 strings of length 20. Which filter is better? The probability of a random false positive for the k -mer filter is 10/ s 10 and for the neighborhood filter it is 800/ s 20. Thus the later filter produces s 10/80 fewer false positives. If s is 4 (e.g. the DNA alphabet) and n is 3109 (e.g. the size of the human genome) then the neighborhood filter produces 13,000 times fewer false positives, and reports in expectation 2.18 false positive, whereas the k -mer filter reports over 28,600!