Bla Bajnok Undergraduate Texts in Mathematics An Invitation to Abstract Mathematics 2013 10.1007/978-1-4614-6636-9_1 Bla Bajnok 2013
1. Lets Play a Game!
We start our friendship with abstract mathematics with an example that illuminates how concrete quantitative problems may turn into abstract mathematical situations and how mathematicians might be led from specific questions to the development of highly abstract concepts and discoveries.
We should admit right away that not all abstractions have an immediate application; indeed, many branches of mathematics were born and developed independently of the real world. Some of these areas later found critical uses; for example, number theory, dubbed by Carl Friedrich Gauss (17771855) as the Queen of Mathematics but long considered arcane, is now playing major roles in computer technology. Other areas, particularly those recently developed, are still waiting for applications.
Our example comes from the interesting, newly developing field of combinatorial game theory. We have simplified the problem as much as possible to reduce technicalities and make our computations simpler. Yet this particular gameand the more challenging (yet, more interesting) games introduced in the problems at the end of this chapterwill enable us later on to discuss some of the most fundamental elements of abstract mathematics, both its objects of study (e.g., the mathematical structures of an abelian group and of a field) and its methods (logic, quantifiers, proof techniques, and more). In fact, at the end of our journey, once we develop the necessary tools, we will return to these games to provide a more thorough and far-reaching analysis to see how we can compare games to one another and decide, for example, when one game is more advantageous for a particular player than another game! This will lead us to a deeper understanding of numbers (zero, positive and negative integers, rational numbers, real numbers, and surreal numbers). As the title of declares, games are value-able!
To begin, let us consider the following situation. Suppose that there is a group of competing companies, all trying to gain control of a certain segment of the market. Each company has a number of possible options that it can carry out (such as introducing or terminating a product and changing prices). These options typically have a limiting effect on one another; in other words, once an option (or a set of options) has been carried out by a certain company (or companies), it prevents another company (or perhaps the same company) from exercising some of its options later.
In our specific example we have two companies, A (Apple Core Corp.) and B (Blue Ink, Inc.), with company A having three available options, which we denote by a 1, a 2, and a 3, and company B having another three available options, denoted by b 1, b 2, and b 3. Let us assume that the restrictions are as follows:
b 3 is available only if a 3 is still available.
a 3 is available only if at least one of b 1 or b 2 is still available.
b 2 is available only if at least one of a 1, a 2, or b 1 is still available.
We assume that the two companies take turns carrying out their options, with each company having to exercise one of its options when it is its turn (each option can only be performed once). The first company unable to exercise any of its options loses. Our question: Which of the two companies is in a better position when the game starts?
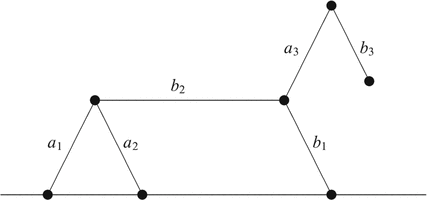
It is helpful to model our game with the following figure:
The figure shows the six options arranged to form a horse. A move will be reflected by removing the corresponding segment from the figure, and the restrictions listed above will be seen by the fact that when certain segments are removed, then some other segments get disconnected from the base. For example, the first restriction means that if we remove the neck of the horse, then its head gets cut off. It is easy to check that our figure reflects all three of our restrictions and no others. As we play our game, we will regard segments disconnected from the ground as unavailable options.
Let us see now how we can analyze this game that we call Aerion (after the horse with the same name in Greek mythology). Note that we did not specify above which company, or player from now on, starts the game. Is the winner going to depend on that? In many games it certainly does.
We will see, however, that no matter who starts Aerion , A has a way to win against B no matter how B plays. To see this, we check all possibilities as follows.
Assume first that A starts. One (and, as we will see shortly, the best) choice for A is to remove a 3 first. Then b 3 becomes unavailable for B , and the game reduces to the following:
Now both A and B have two available options, and it is B s turn. No matter how B moves, the game will terminate in two more rounds, and it will be B who will first run out of options. Thus we see that if A starts, then for any sequence of moves by B , A has some maybe not always the sameway of responding that guarantees a win for A . We describe this situation by saying that A has a winning strategy .
What if B has the chance to move first? If B starts by removing b 3, then A can respond by removing a 3, and the game reduces to the one that we just analyzed, and B loses. The other two initial options are even worse for B , since A will again respond by removing a 3, and the game will terminate in just one more round by B running out of options. Again, A has some winning sequence of moves for every sequence of moves by B . We see, therefore, that no matter who starts our game, A will be able to win no matter how B plays. We can say that this game is a win forA .
We can similarly analyze larger games, but it is not hard to imagine that our arguments become complicated as the number of options and restrictions increases. There is a more systematic approach which, though only after some rather tedious work, makes the conclusion clear. This approach uses the so-called decision trees.
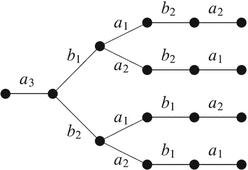
Part of the decision tree of our game, showing all possible plays that start with A starting the game by removing a 3, is shown below. The figure is read from left to right and shows all possible moves at each round. We see that A can win the game in all cases.
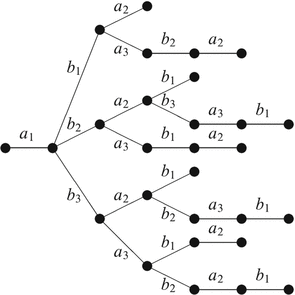
In comparison, consider the next figure, which shows all possible plays if A starts by removing a 1.
We see from the tree that in this case B has a winning strategy. Namely, if B removes b 3, then A loses whether it plays a 2 or a 3 (in the latter case, B should respond by removing b 2). The situation is similar if A s initial move is a 2; B again will win if it responds by b 3. Thus, B has some winning strategy against some initial moves on A s part. However, we saw that the game is a win for A ; that is, if A plays optimally, the game is won by A regardless of who starts the game or how B plays.