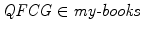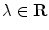John Vince Undergraduate Topics in Computer Science Mathematics for Computer Graphics 4th ed. 2014 10.1007/978-1-4471-6290-2_1
Springer-Verlag London 2014
1. Mathematics
Abstract
Chapter 1 describes the aims and objectives of the book, which are to introduce a range of mathematical topics, without employing too many mathematical symbols and abstract ideas, and provide programmers, animators and technical directors with sufficient confidence and knowledge of mathematics, that they can understand and resolve many of the problems encountered in their day-to-day work.
Advice is also given on the books readership, their background and how to access the different chapters.
1.1 Aims and Objectives of This Book
The aim of this book is to introduce a range of mathematical topics, without employing too many mathematical symbols and abstract ideas. The objective of the book is to provide programmers, animators and technical directors with sufficient confidence and knowledge of mathematics, that they can understand and resolve many of the problems encountered in their day-to-day work.
Each chapter introduces the reader to a new topic, and should give them the confidence to study more advanced texts. I have tried to explain each topic in a simple and practical manner, employing a variety of worked examples.
1.2 Who Should Read This Book?
Increasingly, there are situations and projects that require animators, programmers and technical directors to resort to mathematics to resolve unforeseen technical problems; this may be in the form of a script or an extra piece of program code. Consequently, I have written this book as a reference for anyone intending to study computer graphics, computer animation, computer games or virtual reality, especially for those who want to understand the mathematics behind the technical aspects.
1.3 Assumptions Made in This Book
I assume that readers possess an understanding of arithmetic and a general knowledge of the principles of mathematics, such as algebra, trigonometry and geometry. Apart from that, each subject is introduced as though it were the first time it had been discovered.
1.4 How to Use the Book
I would advise starting at the beginning and proceeding chapter by chapter. Where a subject seems familiar, just jump ahead until a challenge is discovered. Once you have read the book, keep it handy so that you can refer to it when the occasion arises.
Although I have tried to maintain a sequence to the mathematical ideas, so that one idea leads to another, in some cases this has proved impossible. For example, determinants are referred to in the chapter on vectors, but they are described in detail in the next chapter on transforms. Similarly, the later chapter on analytic geometry contains some basic ideas of geometry, but its position was dictated by the use of vectors. Consequently, on some occasions, the reader will have to move between chapters to read about related topics.
1.5 Is Mathematics Difficult?
Is mathematics difficult? I suppose that there is no real answer to this question, because it all depends upon what we mean by mathematics and difficult. But if the question is rephrased slightly: Is the mathematics of computer graphics difficult? then the answer is a definite no. Whats more, I believe that the subject of computer graphics can instil in someone a love for mathematics. Perhaps love is too strong a word, but I am convinced that it is possible to make friends with mathematics.
For me, mathematics should be treated like a foreign language: you only require to learn an appropriate vocabulary to survive while visiting another country. If you attempt to memorise an extended vocabulary, and do not put it to practice, it is highly likely that you will forget it. Mathematics is the same. I know that if I attempted to memorise some obscure branch of mathematics, such as vector calculus, I would forget it within days if I did not put it to some practical use.
John Vince Undergraduate Topics in Computer Science Mathematics for Computer Graphics 4th ed. 2014 10.1007/978-1-4471-6290-2_2
Springer-Verlag London 2014
2. Numbers
Abstract
Numbers are at the heart of mathematics. Some, like prime numbers, are enigmatic, and defy all attempts to predict their arrival; while others, like integers, are well behaved, and can be counted on! This chapter revises some basic ideas about numbers and how we refer to them in the context of mathematics for computer graphics. In particular, I include: natural, prime, integer, rational, irrational, real, imaginary and complex numbers. I also provide a short description on set notation, and our positional number system.
2.1 Introduction
Numbers are at the heart of mathematics. Some, like prime numbers, are enigmatic, and defy all attempts to predict their arrival; while others, like integers, are well behaved, and can be counted on! This chapter revises some basic ideas about numbers and how we refer to them in the context of mathematics for computer graphics. In particular, I include: natural, prime, integer, rational, irrational, real, imaginary and complex numbers. I also provide a short description on set notation, and our positional number system.
2.2 Background
Over the centuries, mathematicians have realised that in order to progress, they must give precise definitions to their discoveries, ideas and concepts, so that they can be built upon and referenced by new mathematical inventions. In the event of any new discovery, these definitions have to be occasionally changed or extended. For example, once upon a time, integers, rational and irrational numbers, satisfied all the needs of mathematicians, until imaginary quantities were invented. Today, complex numbers have helped shape the current number system hierarchy. Consequently, there must be clear definitions for numbers, and the operators that act upon them. Therefore, we need to identify the types of numbers that exist, what they are used for, and any problems that arise when they are stored in a computer.
2.3 Set Notation
A set is a collection of related things identified by a unique name. For example, I own a set of books stored in my library, and a set of photographs stored on my computer. I could call them my-books and my-photos . Similarly, numbers are organised into sets represented by a single letter such as R for reals and Z for integers.
Set theory provides a logical framework for manipulating and interrogating sets, which does not concern us here, apart from the statement confirming that something is a member of a set. For example, the symbol means is a member of, which permits me to state
where QFCG stands for my book Quaternions for Computer Graphics .
It is also common practice to use a symbol such as (lambda), to define a number as follows:
which means that is a member of the set of real numbers R , and is thus a real quantity.