John Vince
Bournemouth University, Poole, UK
ISBN 978-1-4471-7508-7 e-ISBN 978-1-4471-7509-4
https://doi.org/10.1007/978-1-4471-7509-4
Springer-Verlag London Ltd., part of Springer Nature 2021
The author(s) has/have asserted their right(s) to be identified as the author(s) of this work in accordance with the Copyright, Designs and Patents Act 1988.
This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.
The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.
The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, expressed or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This Springer imprint is published by the registered company Springer-Verlag London Ltd. part of Springer Nature.
The registered company address is: The Campus, 4 Crinan Street, London, N1 9XW, United Kingdom
Preface
When I was studying to be an electrical engineer, I came across complex numbers, which were used to represent out-of-phase voltages and currents using the 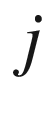 operator. I believe that the letter
operator. I believe that the letter 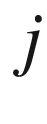 was used, rather than
was used, rather than 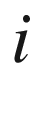 , because the latter stood for electrical current. So from the very start of my studies, I had a clear mental picture of the imaginary unit as a rotational operator which could advance or retard electrical quantities in time.
, because the latter stood for electrical current. So from the very start of my studies, I had a clear mental picture of the imaginary unit as a rotational operator which could advance or retard electrical quantities in time.
When events dictated that I would pursue a career in computer programmingrather than electrical engineeringI had no need for complex numbers, until Mandlebrots work on fractals emerged. But that was a temporary phase, and I never needed to employ complex numbers in any of my computer graphics software. However in 1986, when I joined the flight simulation industry, I came across an internal report on quaternions, which were being used to control the rotational orientation of a simulated aircraft.
I can still remember being completely bemused by quaternions, simply because they involved so many imaginary terms. However, after much research, I started to understand what they were, but not how they worked. Simultaneously, I was becoming interested in the philosophical side of mathematics and trying to come to terms with the real meaning of mathematics through the writing of Bertrand Russell. Consequently, concepts such as 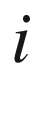 were an intellectual challenge.
were an intellectual challenge.
I am now comfortable with the idea that imaginary 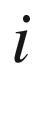 is nothing more than a symbol, and in the context of algebra permits
is nothing more than a symbol, and in the context of algebra permits 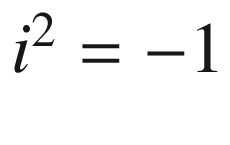 to be defined. And I believe it is futile trying to discover any deeper meaning to its existence. Nevertheless, it is an amazing object within mathematics, and I often wonder whether there could be similar objects waiting to be invented.
to be defined. And I believe it is futile trying to discover any deeper meaning to its existence. Nevertheless, it is an amazing object within mathematics, and I often wonder whether there could be similar objects waiting to be invented.
When I started writing books on mathematics for computer graphics, I studied complex analysis in order to write with some confidence about complex quantities. It was then that I discovered the historical events behind the invention of vectors and quaternions, mainly through Michael Crowes excellent book: A History of Vector Analysis. This book brought home to me the importance of understanding how and why mathematical invention takes place.
I then came across Simon Altmanns book: Rotations, Quaternions, and Double Groups which provided further information concerning the demise of quaternions in the nineteenth century. Altmann is very passionate about securing recognition for the mathematical work of Olinde Rodrigues, who published a formula that is very similar to that generated by Hamiltons quaternions. The important aspect of Rodrigues publication was that it was made three years before Hamiltons invention of quaternions in 1843. However, Rodrigues did not invent quaternion algebrathat prize must go to Hamiltonbut he did understand the importance of half-angles in the trigonometric functions used to rotate points about an arbitrary axis.
Anyone who has used the Euler transforms will be aware of their shortcomings, especially their Achilles heel: gimbal lock. Therefore, any device that can rotate points about an arbitrary axis is a welcome addition to a programmers toolkit. There are many techniques for rotating points and frames in the plane and space, which I covered in some detail in my book: Rotation Transforms for Computer Graphics. That book also covers the Euler-Rodrigues parameterisation and quaternions, but it was only after submitting the manuscript for publication, that I decided to write this book dedicated to quaternions and how and why they were invented and their application to computer graphics.
Whilst researching this book, it was extremely instructive to read some of the early books and papers by William Rowan Hamilton and his friend P. G. Tait. I now understand how difficult it must have been to fully comprehend the significance of quaternion, and how they could be harnessed. At the time, there was no major demand to rotate points about an arbitrary axis; however, a mathematical system was required to handle vectorial quantities. In the end, quaternions were not the flavour of the month and slowly faded from the scene. Nevertheless, the ability to represent vectors and manipulate them arithmetically was a major achievement for Hamilton, even though it was the foresight of Josiah Gibbs to create a simple and workable algebraic framework.













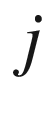 operator. I believe that the letter
operator. I believe that the letter 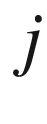 was used, rather than
was used, rather than 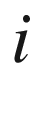 , because the latter stood for electrical current. So from the very start of my studies, I had a clear mental picture of the imaginary unit as a rotational operator which could advance or retard electrical quantities in time.
, because the latter stood for electrical current. So from the very start of my studies, I had a clear mental picture of the imaginary unit as a rotational operator which could advance or retard electrical quantities in time.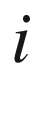 were an intellectual challenge.
were an intellectual challenge.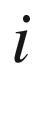 is nothing more than a symbol, and in the context of algebra permits
is nothing more than a symbol, and in the context of algebra permits 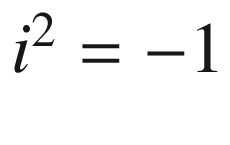 to be defined. And I believe it is futile trying to discover any deeper meaning to its existence. Nevertheless, it is an amazing object within mathematics, and I often wonder whether there could be similar objects waiting to be invented.
to be defined. And I believe it is futile trying to discover any deeper meaning to its existence. Nevertheless, it is an amazing object within mathematics, and I often wonder whether there could be similar objects waiting to be invented.