Dylan Jones and Mehrdad Tamiz International Series in Operations Research & Management Science Practical Goal Programming 10.1007/978-1-4419-5771-9_1
Springer Science+Business Media, LLC 2010
1. History and Philosophy of Goal Programming
Dylan Jones 1
(1)
Logistics and Management Mathematics Group, Department of Mathematics, University of Portsmouth, Lion Gate Building, Lion Terrace, Portsmouth, UK, PO1 3HF
(2)
College of Business Administration, Department of Quantitative Methods and Information Systems, Kuwait University, P.O. Box 5486, Safat, 13055, Kuwait
Dylan Jones (Corresponding author)
Email:
Abstract
The above quote demonstrates that goal-based behaviour and decision making has a long history. This goal-based philosophy has been formalised in the modern field of operational research and management science by the technique of goal programming. The earliest goal programming formulation was introduced by Charnes et al.
Man is a goal seeking animal. His life only has meaning if he is reaching out and striving for his goals .
Aristotle 384322 BC
The above quote demonstrates that goal-based behaviour and decision making has a long history. This goal-based philosophy has been formalised in the modern field of operational research and management science by the technique of goal programming. The earliest goal programming formulation was introduced by Charnes et al. (1955) in the context of executive compensation. At that point the term goal programming was not used and the model was seen as an adaptation of linear programming. A more formal theory of goal programming is given by Charnes and Cooper (1961). Further development took place by Ijiri (1965), and seminal textbooks by Lee (1972) and Ignizio (1976) brought the technique into common usage as an operational research tool. This led to large number of applications being reported in the literature from the mid-1970 onwards. The relatively straightforward ease of which a goal programme could be formulated and the familiarity of practitioners and academics with linear programming methodology ensured that goal programming quickly rose to become the most popular technique within the field of multi-criteria decision making (MCDM). This also, however, brought problems. Although goal programming can correctly be viewed as a generalisation of linear programming, it is also a bona fide multi-criteria decision-making technique. Therefore, users of goal programming should be aware of the theories, methodologies, and pitfalls of multiple criteria decision making if they are to build effective models. Thus goal programming came under criticism in the 1980s because of some basic errors caused, in our opinion, by lack of awareness of good MCDM practice. These included the generation of Pareto-inefficient solutions, the use of excessive numbers of priority levels leading to redundancy, lack of weight sensitivity analysis, direct comparison of incommensurable goals, and ineffectual elicitation and representation of decision maker preferences. This debate culminated in the publication of a key textbook by Romero (1991) in which good goal programming practice is detailed and the problems shown to be due more to poor modelling practice rather than any fundamental deficiency in goal programming.
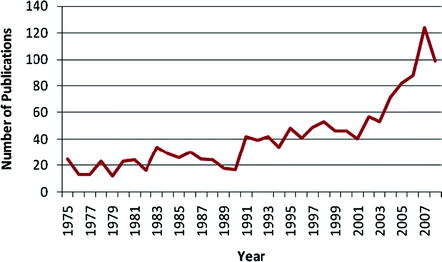
During the 1990s there were further theoretical developments and more complex and varied applications of goal programming. Greater awareness of the multiple criteria aspects of goal programming was in evidence in portions of the literature, with more care being taken to avoid the modelling pitfalls outlined by Romero (1991). There were advances in the user-friendliness of computer software, with the introduction of the GPSYS system which had automated checking for many common modelling errors as well as suggesting ways of overcoming them (Jones et al., 1997). In addition, modern mathematical programming modelling and solution systems made it easier to model and solve all variants of goal programming. Goal programming was combined with other techniques from MCDM and the wider field of operational research with symbiotic advantages. This has been termed the trend of integration and combination and will be further explored in shows an increasing use of goal programming in the early to mid-2000s, with a wide variety of modern fields of application utilising the simplicity and power of the technique.
Fig. 1.1
Goal programming publications in the period 19752008. Source: ISI Web of Knowledge, published by Thomson Reuters
1.1 Terminology
The plethora of terminology used in the field of MCDM can be confusing, with Ehrgott (2005) listing eight different variants of the most fundamental definitions in the field. This section therefore details the basic definitions and concepts from the fields of MCDM and mathematical programming pertaining to goal programming that will be used throughout this book. These concepts will be developed further and brought together algebraically in .
Definition 1.1 Decision Maker(s):
The decision maker(s) in this text refer to the person(s), organisation(s), or stakeholder(s) to whom the decision problem under consideration belongs. For a description of group and organisational decision-making processes in the case of multiple decision makers the reader is referred to French et al. (2009).
Definition 1.2 Decision Variable:
A decision variable is defined as a factor over which the decision maker has control. An example is a manufacturing company which has to decide how many of a certain product to make in the next month. The set of decision variables fully describe the problem and form the decision to be made. The purpose of the goal programming model can be viewed as a search of all the possible combinations of decision variable values (known as decision space) in order to determine the point which best satisfies the decision makers goals and constraints. Figure 3.1 in is an example of a graph drawn in decision space.
Definition 1.3 Criterion:
A criterion is a single measure by which the goodness of any solution to a decision problem can be measured. There are many possible criteria arising from different fields of application but some of the most commonly arising relate at the highest level to
A decision problem which has more than one criterion is therefore referred to as a multi-criteria decision making (MCDM) or multi-criteria decision aid (MCDA) problem. The space formed by the set of criteria is known as criteria space.
Definition 1.4 Objective:
An objective in this book will be referred to as a criterion with the additional information of the direction (maximise or minimise) in which the decision maker(s) prefer on the criterion scale, for example minimise cost or maximise the performance of a system. A decision problem with a set of objectives to be maximised or minimised is referred to as a multi-objective optimisation problem . In practice, these objectives will be conflicting, that is they cannot reach their optimal values simultaneously. If they could, then the model can be solved as a single-objective problem for any of the objectives. The space formed by the values of the set of objectives is known as objective space. Figure shows an example of objective space for a bi-objective decision problem.