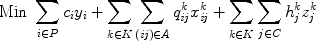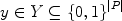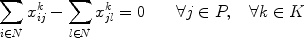Introduction
A supply chain (SC) is a network of suppliers, manufacturing plants, warehouses, and distribution channels organized to acquire raw materials, convert these raw materials to finished products, and distribute these products to customers. The concept of supply chain management (SCM), which appeared in the early 1990s, has recently raised a lot of interest since the opportunity of an integrated management of the supply chain can reduce the propagation of unexpected/undesirable events through the network and can affect decisively the profitability of all the members.
A crucial component of the planning activities of a manufacturing firm is the efficient design and operation of its supply chain. Strategic level supply chain planning involves deciding the configuration of the network, i.e., the number, location, capacity, and technology of the facilities. The tactical level planning of supply chain operations involves deciding the aggregate quantities and material flows for purchasing, processing, and distribution of products. The strategic configuration of the supply chain is a key factor influencing efficient tactical operations, and therefore has a long lasting impact on the firm. Furthermore, the fact that the supply chain configuration involves the commitment of substantial capital resources over long periods of time makes the supply chain design problem an extremely important one.
Many attempts have been made to model and optimize supply chain design, most of which are based on deterministic approaches, see for example Bok et al. (), and many others. However, most real supply chain design problems are characterized by numerous sources of technical and commercial uncertainty, and so the assumption that all model parameters, such as cost coefficients, supplies, demands, etc., are known with certainty is not realistic.
In order to take into account the effects of the uncertainty in the production scenario, a two-stage stochastic model is proposed in this paper. Decision variables which characterize the network configuration, namely those binary variables which represent the existence and the location of plants and warehouses of the supply chain are considered as first-stage variables it is assumed that they have to be taken at the strategic level before the realization of the uncertainty. On the other hand, decision variables related to the amount of products to be produced and stored in the nodes of the supply chain and the flows of materials transported among the entities of the network are considered as second-stage variables, corresponding to decisions taken at the tactical level after the uncertain parameters have been revealed.
There are a few research works addressing comprehensive (strategic and tactical issues simultaneously) design of supply chain networks using two-stage stochastic models. MirHassani et al. () integrated a sampling strategy with an accelerated Benders decomposition to solve supply chain design problems with continuous distributions for the uncertain parameters. However, the robustness of decision to uncertain parameters is not considered in above studies.
Azaron et al. () for details, to solve the resulting multi-objective problem.
This method has the same disadvantages as those of goal programming; namely, the preferred solution is sensitive to the goal vector and the weighting vector given by the decision maker. To overcome this drawback, we also use interactive multi-objective techniques with explicit or implicit trade-off information given such as SWT and STEM methods, see Hwang and Masud () is that we minimize downside risk or risk of loss instead of financial risk. By applying this concept, we avoid the use of binary variables to determine the financial risk, which significantly reduces the computational time to solve the final large scale mixed-integer nonlinear programming problem.
To the best of our knowledge, only -constraint method (Guillen et al. ) have been used to solve existing multi-objective supply chain design models. In this paper, we use interactive multi-objective techniques to solve the problem.
The paper is organized as follows. In Sect..
Problem Description
We first describe a deterministic mathematical formulation for the supply chain design problem. Consider a supply chain network G = ( N , A ), where N is the set of nodes and A is the set of arcs. The set N consists of the set of suppliers S , the set of possible processing facilities P , and the set of customer centers C , i.e., N = S P C . The processing facilities include manufacturing centers M and warehouses W , i.e., P = M W . Let K be the set of products flowing through the supply chain.
The supply chain configuration decisions consist of deciding which of the processing centers to build. We associate a binary variable y i to these decisions: y i = 1 if processing facility i is built, and 0 otherwise. The tactical decisions consist of routing the flow of each product k K from the suppliers to the customers. We let
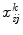
denote the flow of product k from a node i to a node j of the network where ( ij ) A , and
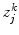
denote shortfall of product k at customer centre j , when it is impossible to meet demand. A deterministic mathematical model for this supply chain design problem is formulated as follows (see Santoso et al. () for more details):
s.t.












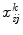 denote the flow of product k from a node i to a node j of the network where ( ij ) A , and
denote the flow of product k from a node i to a node j of the network where ( ij ) A , and 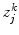 denote shortfall of product k at customer centre j , when it is impossible to meet demand. A deterministic mathematical model for this supply chain design problem is formulated as follows (see Santoso et al. () for more details):
denote shortfall of product k at customer centre j , when it is impossible to meet demand. A deterministic mathematical model for this supply chain design problem is formulated as follows (see Santoso et al. () for more details):