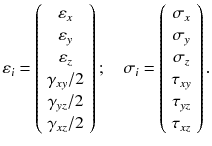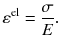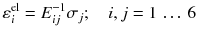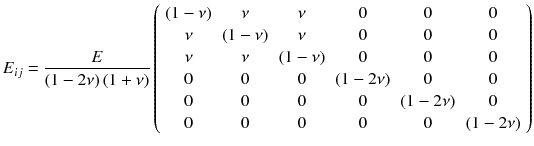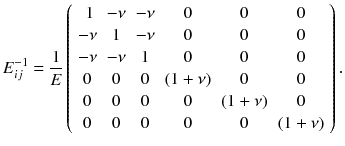Some basics of plastic material behavior and approaches to its mathematical description by material models are outlined, as well as the impact on the behavior of elastic-plastic structures.
1.1 Plastic Reserve
Because of its high elongation at break of usually more than 20 %, steel material has a large plastic reserve compared to its elastic limit strain of usually far less than 1 %. With respect to the elastic limit stress, the plastic reserve is far lower. Accordingly, the plastic reserve for displacement-controlled loading is much larger than for force-controlled loading.
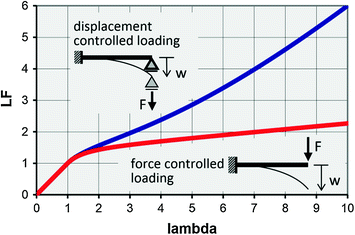
This is exemplarily illustrated in Fig. for a cantilever beam, loaded force-controlled at the free end by a concentrated load or displacement-controlled because of a support displacement causing a concentrated force as a support reaction. The load factor (LF) is shown as a multiple of the elastic limit load over the multiple of the elastic limit strain (lambda). Force-controlled and displacement-controlled loads are indistinguishable from each other in the elastic range (LF 1, lambda 1). In the plastic range, however, a higher load level belongs to a given strain for displacement-controlled than for force-controlled loading.
Fig. 1.1
Plastic reserve for a cantilever beam subjected to displacement-controlled and force-controlled loading (applies to a cantilever with rectangular cross-section made of a linear hardening material (hardening parameter C/E = 0.1) if limited to the theory of small displacements and small rotations)
Especially in the case of displacement-controlled loading, load levels much higher than the elastic limit load may be applied because of the ductility of the material. Displacement-controlled loading is not only represented by the support displacements considered above but can also consist of thermal expansion. Therefore the plastic reserve is particularly exploited in thermal power plants, where the temperature fields resulting from changeable operating conditions may cause considerable strains. Assuming linear elastic material behavior, i.e., calculated fictitious elastic, they can easily exceed 12 times the yield strength of the steel structure.
Displacement-controlled loading not only results from preventing thermal expansion but may also be attributed to reaction forces and section forces not required for equilibrium but only to maintain continuity of the structure in statically indeterminate structures. Apart from a few special structures such as membrane shells, two- and three-dimensional continua are internally statically indeterminate. There is therefore almost always a plastic reserve, even if these structures are primarily subject to a force-controlled load.
If structures are operated beyond the elastic range, it is not only necessary to ensure that the ductility of the material produced by monotonically increasing loading is not exceeded. It should also be noted that even small variable load portions can set in motion a mechanism which leads to a one-way increase in elongation at any load change, thus limiting the service life of the structure. Such a process is often called ratcheting (frequently also spelled ratchetting) or referred to as progressive deformation. It is explained in detail in Chap..
In addition, fatigue damage can occur, especially if the strain range is so large that there is alternating plasticity (low cycle fatigue, LCF). However, because portions of the load are always variable, ratcheting should always be taken into account whenever plastic straining occurs, and not only if the variable loading is high enough for alternating plasticity to occur.
The matters covered in this book are not only relevant to thermal power plants, but also to many applications in civil engineering, such as bridge bearings and road surfaces as well as geotechnical engineering. Moreover, ratcheting and LCF can already occur under normal design conditions in mechanical engineering and vehicle construction, in the chemical industry, in gas turbines, and in many other applications. These phenomena may also play a role when guarding against limit states.
To take advantage of the ductility of the material is not restricted to steel but increasingly also to materials with a significantly lower ductility than steel, such as concrete or soil.
1.2 Basic Concepts of Modeling Plastic Material Behavior
In this section, some terms related to plastic material behavior are explained, which are important for the understanding of the STPZ. It is not intended here to explain the thermodynamic or microscopic fundamentals of the theory of plasticity or to represent their extensive phenomenology. However, the following descriptions should suffice to allow interested readers to be able to carry out their own research if necessary. As an introduction to a more detailed treatment of the material-mechanical fundamentals of the theory of plasticity, the reader is referred to the book by Lemaitre and Chaboche [].
The mechanical behavior of materials is described by material models and captured mathematically by constitutive equations, describing the relationship between the six components of strain and the six components of stress:
1.2.1 Elastic Behavior
The simplest material model is Hookes law, describing linear elastic behavior. Nonlinear elastic and viscoelastic behavior, which can be used to describe elastic hysteresis effects, is not considered in the following, however. Hookes law gives a direct relationship between the stress and strain components. In case of a uniaxial stress and isotropic material behavior we get for the elastic strain el acting in the same direction
If the isotropic material is subjected to a multiaxial stress we need to make use of a second elastic material parameter beside Youngs modulus E , the Poissons ratio :
In this notation, use is made of the so-called summation convention, which means that summation is to be performed over indices appearing twice in a term, i.e., over j in Eq. ().
Up to 21 different parameters are required to describe its linear elastic behavior if the material is anisotropic.